from IPython.display import Image
Image('../../Python_probability_statistics_machine_learning_2E.png',width=200)
Useful Distributions¶
Normal Distribution¶
Without a doubt, the normal (Gaussian) distribution is the most important and foundational probability distribution. The one-dimensional form is the following:
$$ f(x) =\frac{e^{-\frac{(x-\mu)^2}{2\sigma^2}}}{\sqrt{2\pi\sigma^2 } } $$where $\mathbb{E}(x)=\mu$ and $\mathbb{V}(x)=\sigma^2$. The multidimensional version for $\mathbf{x}\in \mathbb{R}^n$ is the following,
$$ f(\mathbf{x}) = \frac{1}{\det(2\pi \mathbf{R})^{\frac{1}{2}}} e^{-\frac{1}{2}(\mathbf{x}-\boldsymbol{\mu})^T \mathbf{R}^{-1}(\mathbf{x}-\boldsymbol{\mu})} $$where $\mathbf{R}$ is the covariance matrix with entries
$$ R_{i,j} = \mathbb{E}\left[ (x_i-\bar{x_i})(x_j-\bar{x_j}) \right] $$A key property of the normal distribution is that it is completely specified by its first two moments. Another key property is that the normal distribution is preserved under linear tranformations. For example,
$$ \mathbf{y} = \mathbf{A x} $$means $\mathbf{y}\sim \mathcal{N}(\mathbf{A x},\mathbf{A R_x} \mathbf{A}^T)$. This means that it is easy to do linear algebra and matrix operations with normal distributed random variables. There are many intuitive geometric relationships that are preserved with normal distributed random variables, as discussed in the Gauss-Markov chapter.
Multinomial Distribution¶
The Multinomial distribution generalized the Binomial
distribution.
Recall that the Binomial distribution characterizes the number of
heads obtained
in $n$ trials.
Consider the problem of $n$ balls to be divided
among $r$ available bins
where each bin may accommodate more than one ball. For
example, suppose
$n=10$ and and $r=3$, then one possible valid configuration is
$\mathbf{N}_{10}=[3,3,4]$. The probability that a ball lands in the
$i^{th}$ bin
is $p_i$, where $\sum p_i=1$. The Multinomial distribution
characterizes the
probability distribution of $\mathbf{N}_n$. The Binomial
distribution is a
special case of the Multinomial distribution with $n=2$. The
Multinomial
distribution is implmented in the scipy.stats module as shown
below,
from scipy.stats import multinomial
rv = multinomial(10,[1/3]*3)
rv.rvs(4)
array([[1, 5, 4],
[1, 4, 5],
[4, 2, 4],
[4, 2, 4]])
Note that the sum across the columns is always $n$
rv.rvs(10).sum(axis=1)
array([10, 10, 10, 10, 10, 10, 10, 10, 10, 10])
To derive the probability mass function, we define the occupancy vector, $\mathbf{e}_i\in \mathbb{R}^r$ which is a binary vector with exactly one non- zero component (i.e., a unit vector). Then, the $\mathbf{N}_n$ vector can be written as the sum of $n$ vectors $\mathbf{X}$, each drawn from the set $\lbrace \mathbf{e}_j \rbrace_{j=1}^r$,
$$ \mathbf{N}_n = \sum_{i=1}^n \mathbf{X}_i $$where the probability $\mathbb{P}(\mathbf{X}=\mathbf{e}_j)=p_j$. Thus, $\mathbf{N}_n$ has a discrete distribution over the set of vectors with non- negative components that sum to $n$. Because the $\mathbf{X}$ vectors are independent and identically distributed, the probability of any particular $\mathbf{N}_n=[ x_1,x_2,\cdots,x_r ]^\top=\mathbf{x}$ is
$$ \mathbb{P}(\mathbf{N}_n=x) = C_n p_1^{x_1} p_2^{x_2}\cdots p_r^{x_r} $$where $C_n$ is a combinatorial factor that accounts for all the ways a component can sum to $x_j$. Consider that there are $\binom{n}{x_1}$ ways that the first component can be chosen. This leaves $n-x_1$ balls left for the rest of the vector components. Thus, the second component has $\binom{n-x_1}{x_2}$ ways to pick a ball. Following the same pattern, the third component has $\binom{n-x_1-x_2}{x_3}$ ways and so forth,
$$ C_n = \binom{n}{x_1}\binom{n-x_1}{x_2} \binom{n-x_1-x_2}{x_3} \cdots \binom{n-x_1-x_2-\cdots-x_{r-1}}{x_r} $$simplifies to the following,
$$ C_n = \frac{n!}{x_1! \cdots x_r!} $$Thus, the probability mass function for the Multinomial distribution is the following,
$$ \mathbb{P}(\mathbf{N}_n=x) = \frac{n!}{x_1! \cdots x_r!} p_1^{x_1} p_2^{x_2}\cdots p_r^{x_r} $$The expectation of this distribution is the following,
$$ \mathbb{E}(\mathbf{N}_n) = \sum_{i=1}^n \mathbb{E}(X_i) $$by the linearity of the expectation. Then,
$$ \mathbb{E}(X_i) = \sum_{j=1}^r p_j \mathbf{e}_j = \mathbf{I}\mathbf{p}=\mathbf{p} $$where $p_j$ are the components of the vector $\mathbf{p}$ and $\mathbf{I}$ is the identity matrix. Then, because this is the same for any $X_i$, we have
$$ \mathbb{E}(\mathbf{N}_n) = n \mathbf{p} $$For the covariance of $\mathbf{N}_n$, we need to compute the following,
$$ \textrm{Cov}(\mathbf{N}_n) = \mathbb{E}\left(\mathbf{N}_n \mathbf{N}_n^\top\right) - \mathbb{E}(\mathbf{N}_n) \mathbb{E}(\mathbf{N}_n)^\top $$For the first term on the right, we have
$$ \mathbb{E}\left(\mathbf{N}_n \mathbf{N}_n^\top\right)=\mathbb{E}\left((\sum_{i=1}^n X_i)(\sum_{j=1}^n X_j^\top) \right) $$and for $i=j$, we have
$$ \mathbb{E}(X_i X_i^\top) = \textrm{diag}(\mathbf{p}) $$and for $i\neq j$, we have
$$ \mathbb{E}(X_i X_j^\top) = \mathbf{p}\mathbf{p}^\top $$Note that this term has elements on the diagonal. Then, combining the above two equations gives the following,
$$ \mathbb{E}(\mathbf{N}_n\mathbf{N}_n^\top) = n \textrm{diag}(\mathbf{p}) + (n^2-n) \mathbf{p}\mathbf{p}^\top $$Now, we can assemble the covariance matrix,
$$ \textrm{Cov}(\mathbf{N}_n) = n \textrm{diag}(\mathbf{p}) + (n^2-n) \mathbf{p}\mathbf{p}^\top - n^2 \mathbf{p} \mathbf{p}^\top = n \textrm{diag}(\mathbf{p})-n \mathbf{p} \mathbf{p}^\top $$Specifically, the off-diagonal terms are $n p_i p_j$ and the diagonal terms are $n p_i (1-p_i)$.
Chi-Square Distribution¶
The $\chi^2$ distribution appears in many different contexts so it's worth understanding. Suppose we have $n$ independent random variables $X_i$ such that $X_i\sim \mathcal{N}(0,1)$. We are interested in the following random variable $R = \sqrt{\sum_i X_i^2}$. The joint probability density of $X_i$ is the following,
$$ f_{\mathbf{X}}(X) = \frac{e^{-\frac{1}{2}\sum_i X_i^2}}{(2\pi)^{\frac{n}{2}}} $$where the $\mathbf{X}$ represents a vector of $X_i$ random variables. You can think of $R$ as the radius of an $n$-dimensional sphere. The volume of this sphere is given by the the following formula,
$$ V_n(R) = \frac{\pi^{\frac{n}{2}}}{\Gamma(\frac{n}{2}+1)} R^n $$To reduce the amount of notation we define,
$$ A := \frac{\pi^{\frac{n}{2}}}{\Gamma(\frac{n}{2}+1)} $$The differential of this volume is the following,
$$ dV_n(R)= n A R^{n-1} dR $$In term of the $X_i$ coordinates, the probability (as always) integrates out to one.
$$ \int f_{\mathbf{X}}(\mathbf{X}) dV_n(\mathbf{X}) = 1 $$In terms of $R$, the change of variable provides,
$$ \int f_{\mathbf{X}}(R) n A R^{n-1} dR $$Thus,
$$ f_R(R):=f_{\mathbf{X}}(R) = n A R^{n-1}\frac{e^{-\frac{1}{2}R^2}}{(2\pi)^{\frac{n}{2}}} $$But we are interested in the distribution $Y=R^2$. Using the same technique again,
$$ \int f_{R}(R) dR =\int f_{R}(\sqrt{Y}) \frac{dY}{2\sqrt{Y}} $$Finally,
$$ f_Y(Y) := n A Y^\frac{n-1}{2}\frac{e^{-\frac{1}{2}Y}}{(2\pi)^{\frac{n}{2}}} \frac{1}{2\sqrt{Y}} $$Then, finally substituting back in $A$ gives the $\chi^2$ distribution with $n$ degrees of freedom,
$$ f_Y(Y) = n \frac{\pi^{\frac{n}{2}}}{\Gamma(\frac{n}{2}+1)} Y^{n/2-1}\frac{e^{-\frac{1}{2}Y}}{(2\pi)^{\frac{n}{2}}} \frac{1}{2}= \frac{2^{-\frac{n}{2}-1} n }{\Gamma \left(\frac{n}{2}+1\right)}e^{-Y/2} Y^{\frac{n}{2}-1} $$Example: Hypothesis testing is a common application of the $\chi^2$ distribution. Consider Table 1 which tabulates the infection status of a certain population. The hypothesis is that these data are distributed according to the multinomial distribution with the following rates for each group, $p_1=1/4$ (mild infection), $p_2=1/4$ (strong infection), and $p_3=1/2$ (no infection). Suppose $n_i$ is the count of persons in the $i^{th}$ column and $\sum_{i} n_i=n=684$. Let $k$ denote the number of columns. Then, in order to apply the Central Limit Theorem, we want to sum the $n_i$ random variables, but these all sum to $n$, a constant, which prohibits using the theorem. Instead, suppose we sum the $n_i$ variables up to $k-1$ terms. Then,
$$ z = \sum_{i=1}^{k-1} n_i $$is asymptotically normally distributed by the theorem with mean $\mathbb{E}(z) = \sum_{i=1}^{k-1} n p_i$. Using our previous results and notation for multinomial random variables, we can write this as
$$ z = [\mathbf{1}_{k-1}^\top,0]\mathbf{N}_n $$where $\mathbf{1}_{k-1}$ is a vector of all ones of length $k-1$ and $\mathbf{N}_n\in \mathbb{R}^{k}$. With this notation, we have
$$ \mathbb{E}(z )= n [\mathbf{1}_{k-1}^\top,0] \mathbf{p} = \sum_{i=1}^{k-1} n p_i = n(1-p_k) $$We can get the variance of $z$ using the same method,
$$ \mathbb{V}(z) =[\mathbf{1}_{k-1}^\top,0]\textrm{Cov}(\mathbf{N}_n)[\mathbf{1}_{k-1}^\top,0]^\top $$which gives,
$$ \mathbb{V}(z) =[\mathbf{1}_{k-1}^\top,0](n\textrm{diag}(\mathbf{p})-n\mathbf{p}\mathbf{p}^\top )[\mathbf{1}_{k-1}^\top,0]^\top $$The variance is then,
$$ \mathbb{V}(z) = n (1-p_k)p_k $$With the mean and variance established we can subtract the hypothesize mean for each column under the hypothesis and create the transformed variable,
$$ z^\prime = \sum_{i=1}^{k-1} \frac{n_i-n p_i}{\sqrt{n (1-p_k)p_k}} \sim \mathcal{N}(0,1) $$by the Central Limit Theorem. Likewise,
$$ \sum_{i=1}^{k-1} \frac{(n_i-n p_i)^2}{n (1-p_k)p_k} \sim \chi_{k-1}^2 $$ $$ \begin{table}[] \centering \caption{Diagnosis Table} \label{tab:diagnosisTable} \tag{1} \begin{tabular}{lllll} \cline{1-4} \multicolumn{1}{|l|}{Mild Infection} & \multicolumn{1}{l|}{Strong Infection} & \multicolumn{1}{l|}{No infection} & \multicolumn{1}{l|}{Total} & \\ \cline{1-4} \multicolumn{1}{|c|}{128} & \multicolumn{1}{c|}{136} & \multicolumn{1}{c|}{420} & \multicolumn{1}{c|}{684} & \\ \cline{1-4} \end{tabular} \end{table} $$With all that established, we can test the hypothesis that the data in the table follow the hypothesized multinomial distribution.
from scipy import stats
n = 684
p1 = p2 = 1/4
p3 = 1/2
v = n*p3*(1-p3)
z = (128-n*p1)**2/v + (136-n*p2)**2/v
1-stats.chi2(2).cdf(z)
0.00012486166748693073
This value is very low and suggests that the hypothesized multinomial
distribution is not a good one for this data. Note that this approximation only
works when n is large in comparison to the number of columns in the table.
¶
Poisson and Exponential Distributions
The Poisson distribution for a random variable $X$ represents a number of outcomes occurring in a given time interval ($t$).
$$ p(x;\lambda t) = \frac{e^{-\lambda t}(\lambda t)^x}{x!} $$The Poisson distribution is closely related to the binomial distribution, $b(k;n,p)$ where $p$ is small and $n$ is large. That is, when there is a low- probability event but many trials, $n$. Recall that the binomial distribution is the following,
$$ b(k;n,p) =\binom{n}{k} p^k (1-p)^{n-k} $$for $k=0$ and taking the logarithm of both sides, we obtain
$$ \log b(0;n,p) = (1-p)^n = \left( 1-\frac{\lambda}{n} \right)^n $$Then, the Taylor expansion of this gives the following,
$$ \log b(0;n,p) \approx -\lambda - \frac{\lambda^2}{2 n} - \cdots $$For large $n$, this results in,
$$ b(0;n,p) \approx e^{-\lambda} $$A similar argument for $k$ leads to the Poisson distribution. Conveniently, we have $\mathbb{E}(X) = \mathbb{V}(X)= \lambda$. For example, suppose that the average number of vehicles passing under a toll-gate per hour is 3. Then, the probability that 6 vehicles pass under the gate in a given hour is $p(x=6;\lambda t= 3) = \frac{81}{30 e^3}\approx 0.05$.
The Poisson distribution
is available from the scipy.stats module.
The following code computes the last
result,
from scipy.stats import poisson
x = poisson(3)
print(x.pmf(6))
0.05040940672246224
The Poisson distribution is important for applications involving reliability and queueing. The Poisson distribution is used to compute the probability of specific numbers of events during a particular time period. In many cases the time period ($X$) itself is the random variable. For example, we might be interested in understanding the time $X$ between arrivals of vehicles at a checkpoint. With the Poisson distribution, the probability of no events occurring in the span of time up to time $t$ is given by the following,
$$ p(0;\lambda t) = e^{-\lambda t} $$Now, suppose $X$ is the time to the first event. The probability that the length of time until the first event will exceed $x$ is given by the following,
$$ \mathbb{P}(X>x) = e^{-\lambda x} $$Then, the cumulative distribution function is given by the following,
$$ \mathbb{P}(0\le X\le x) = F_X (x) = 1-e^{- \lambda x} $$Taking the derivative gives the exponential distribution,
$$ f_X(x) = \lambda e^{-\lambda x} $$where $\mathbb{E}(X) = 1/\lambda $ and $\mathbb{V}(X)=\frac{1}{\lambda^2}$.
For
example, suppose we want to know the probability of a certain
component lasting
beyond $T=10$ years where $T$ is modeled as a
an exponential random variable
with $1/\lambda=5$ years. Then, we have
$1-F_X(10) = e^{-2} \approx 0.135 $.
The exponential distribution is available in the scipy.stats module. The
following code computes the result of the example above. Note that the
parameters are described in slightly different terms as above, as described in
the corresponding documentation for expon.
from scipy.stats import expon
x = expon(0,5) # create random variable object
print(1 - x.cdf(10))
0.1353352832366127
Gamma Distribution¶
We have previously discussed how the exponential distribution can be created from the Poisson events. The exponential distribution has the memoryless property, namely,
$$ \mathbb{P}(T>t_0+t\vert T>t_0) = \mathbb{P}(T>t) $$For example, given $T$ as the random variable representing the time until failure, this means that a component that has survived up through $t_0$ has the same failure probability of lasting $t$ units beyond that point. To derive this result, it is easier to compute the complementary event,
$$ \mathbb{P}(t_0<T<t_0+t\vert T>t_0) = \mathbb{P}(t_0<T<t_0+t) = e^{-\lambda t} \left(e^{\lambda t}-1\right) $$Then, one minus this result shows the memoryless property, which, unrealistically, does not account for wear over the first $t$ hours. The gamma distribution can remedy this.
Recall that the exponential distribution describes the time until the occurrence of a Poisson event, the random variable $X$ for the time until a specified number of Poisson events ($\alpha$) is described by the gamma distribution. Thus, the exponential distribution is a special case of the gamma distribution when $\alpha=1$ and $\beta=1/\lambda$. For $x>0$, the gamma distribution is the following,
$$ f(x;\alpha,\beta)= \frac{\beta ^{-\alpha } x^{\alpha -1} e^{-\frac{x}{\beta }}}{\Gamma (\alpha )} $$and $f(x;\alpha,\beta)=0$ when $x\le 0$ and $\Gamma$ is the gamma function. For example, suppose that vehicles passing under a gate follows a Poisson process, with an average of 5 vehicles passing per hour, what is the probability that at most an hour will have passed before 2 vehicles pass the gate? If $X$ is time in hours that transpires before the 2 vehicles pass, then we have $\beta=1/5$ and $\alpha=2$. The required probability $\mathbb{P}(X<1) \approx 0.96 $. The gamma distribution has $\mathbb{E}(X) = \alpha\beta $ and $\mathbb{V}(X)=\alpha\beta^2$
The
following code computes the result of the
example above. Note that the
parameters are described in slightly different
terms as above, as described in
the corresponding documentation for gamma.
from scipy.stats import gamma
x = gamma(2,scale=1/5) # create random variable object
print(x.cdf(1))
0.9595723180054873
Beta Distribution¶
The uniform distribution assigns a single constant value over the unit interval. The Beta distribution generalizes this to a function over the unit interval. The probability density function of the Beta distribution is the following,
$$ f(x ) = \frac{1}{\beta(a,b)} x^{a-1} (1-x)^{b-1} $$where
$$ \beta(a,b) = \int_0^1 x^{a-1} (1-x)^{b-1} dx $$Note that $a=b=1$ yields the uniform distribution. In the special case for integers where $0\le k\le n$, we have
$$ \int_0^1 \binom{n}{k}x^k (1-x)^{n-k} dx = \frac{1}{n+1} $$To get this result without calculus, we can use an experiment by Thomas Bayes. Start with $n$ white balls and one gray ball. Uniformly at random, toss them onto the unit interval. Let $X$ be the number of white balls to the left of the gray ball. Thus, $X\in \lbrace 0,1,\ldots,n \rbrace$. To compute $\mathbb{P}(X=k)$, we condition on the probability of the position $B$ of the gray ball, which is uniformly distributed over the unit interval ($f(p)=1$). Thus, we have
$$ \mathbb{P}(X=k) = \int_0^1 \mathbb{P}(X=k\vert B=p) f(p) dp = \int_0^1 \binom{n}{k}p^k (1-p)^{n-k} dp $$Now, consider a slight variation on the experiment where we start with $n+1$ white balls and again toss them onto the unit interval and then later choose one ball at random to color gray. Using the same $X$ as before, by symmetry, because any one of the $n+1$ balls is equally likely to be chosen, we have
$$ \mathbb{P}(X=k)=\frac{1}{n+1} $$for $k\in \lbrace 0,1,\ldots,n \rbrace$. Both situations describe the same problem because it does not matter whether we paint the ball before or after we throw it. Setting the last two equations equal gives the desired result without using calculus.
$$ \int_0^1 \binom{n}{k}p^k (1-p)^{n-k} dp = \frac{1}{n+1} $$The following code shows where to get the Beta distribution from the scipy
module.
from scipy.stats import beta
x = beta(1,1) # create random variable object
print(x.cdf(1))
1.0
Given this experiment, it is not too surprising that there is an intimate relationship between the Beta distribution and binomial random variables. Suppose we want to estimate the probability of heads for coin-tosses using Bayesian inference. Using this approach, all unknown quantities are treated as random variables. In this case, the probability of heads ($p$) is the unknown quantity that requires a prior distribution. Let us choose the Beta distribution as the prior distribution, $\texttt{Beta}(a,b)$. Then, conditioning on $p$, we have
$$ X\vert p \sim \texttt{binom}(n,p) $$which says that $X$ is conditionally distributed as a binomial. To get the posterior probability, $f(p\vert X=k)$, we have the following Bayes rule,
$$ f(p\vert X=k) = \frac{\mathbb{P}(X=k\vert p)f(p)}{\mathbb{P}(X=k)} $$with the corresponding denominator,
$$ \mathbb{P}(X=k) = \int_0^1 \binom{n}{k}p^k (1-p)^{n-k}f(p) dp $$Note that unlike with our experiment before, $f(p)$ is not constant. Without substituting in all of the distributions, we observe that the posterior is a function of $p$ which means that everything else that is not a function of $p$ is a constant. This gives,
$$ f(p\vert X=k) \propto p^{a+k-1} (1-p)^{b+n-k-1} $$which is another Beta distribution with parameters $a+k,b+n-k$. This special relationship in which the beta prior probability distribution on $p$ on data that are conditionally binomial distributed yields the posterior that is also binomial distributed is known as conjugacy. We say that the Beta distribution is the conjugate prior of the binomial distribution.
Dirichlet-multinomial¶
Distribution
The Dirichlet-multinomial distribution is a discrete multivariate distribution also known as the multivariate Polya distribution. The Dirichlet-multinomial distribution arises in situations where the usual multinomial distribution is inadequate. For example, if a multinomial distribution is used to model the number of balls that land in a set of bins and the multinomial parameter vector (i.e., probabilities of balls landing in particular bins) varies from trial to trial, then the Dirichlet distribution can be used to include variation in those probabilities because the Dirichlet distribution is defined over a simplex that describes the multinomial parameter vector.
Specifically, suppose we have $K$ rival events, each with probability $\mu_k$. Then, the probability of the vector $\boldsymbol{\mu}$ given that each event has been observed $\alpha_k$ times is the following,
$$ \mathbb{P}(\boldsymbol{\mu}\vert \boldsymbol{\alpha}) \propto \prod_{k=1}^K \mu_k^{\alpha_k-1} $$where $0\le\mu_k\le 1$ and $\sum\mu_k=1$. Note that this last sum is a constraint that makes the distribution $K-1$ dimensional. The normalizing constant for this distribution is the multinomial Beta function,
$$ \texttt{Beta}(\boldsymbol{\alpha})=\frac{\prod_{k=1}^K\Gamma(\alpha_k)}{\Gamma(\sum_{k=1}^K\alpha_k)} $$The elements of the $\boldsymbol{\alpha}$ vector are also called
concentration parameters. As before, the Dirichlet
distribution can be found
in the scipy.stats module,
from scipy.stats import dirichlet
d = dirichlet([ 1,1,1 ])
d.rvs(3) # get samples from distribution
array([[0.26430564, 0.12853028, 0.60716408],
[0.19141157, 0.29026109, 0.51832735],
[0.2200943 , 0.13789725, 0.64200845]])
Note that each of the rows sums to one. This is because of the
$\sum\mu_k=1$
constraint. We can generate more samples and plot this
using Axes3D in
Matplotlib in Figure.
%matplotlib inline
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.pyplot import subplots
x = d.rvs(1000)
fig, ax = subplots(subplot_kw=dict(projection='3d'))
_=ax.scatter(x[:,0],x[:,1],x[:,2],marker='o',alpha=.2)
ax.view_init(30, 30) # elevation, azimuth
# ax.set_aspect(1)
_=ax.set_xlabel(r'$\mu_1$')
_=ax.set_ylabel(r'$\mu_2$')
_=ax.set_zlabel(r'$\mu_3$')
fig.savefig('fig-probability/Dirichlet_001.png')
One thousand samples from a Dirichlet distribution with $\boldsymbol{\alpha} = [1,1,1]$
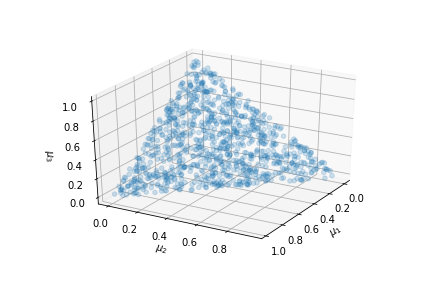
Notice that the
generated samples lie on the triangular simplex shown. The
corners of the
triangle correspond to each of the components in the
$\boldsymbol{\mu}$. Using,
a non-uniform $\boldsymbol{\alpha}=[2,3,4]$ vector,
we can visualize the
probability density function using the pdf method on the
dirichlet object as
shown in Figure. By choosing the
$\boldsymbol{\alpha}\in
\mathbb{R}^3$, the peak of the density function can be
moved within the
corresponding triangular simplex.
import numpy as np
from matplotlib.pylab import cm
X,Y = np.meshgrid(np.linspace(.01,1,50),np.linspace(.01,1,50))
d = dirichlet([2,3,4])
idx=(X+Y<1)
f=d.pdf(np.vstack([X[idx],Y[idx],1-X[idx]-Y[idx]]))
Z = idx*0+ np.nan
Z[idx] = f
fig,ax=subplots()
_=ax.contourf(X,Y,Z,cmap=cm.viridis)
ax.set_aspect(1)
_=ax.set_xlabel('x',fontsize=18)
_=ax.set_ylabel('y',fontsize=18)
fig.savefig('fig-probability/Dirichlet_002.png')
Probability density function for the Dirichlet distribution with $\boldsymbol{\alpha}=[2,3,4]$
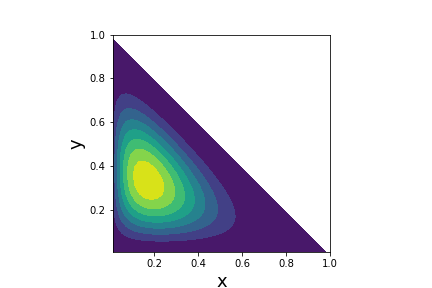
We have seen that the Beta distribution generalizes the uniform distribution over the unit interval. Likewise, the Dirichlet distribution generalizes the Beta distribution over a vector with components in the unit interval. Recall that binomial distribution and the Beta distribution form a conjugate pair for Bayesian inference because with $p\sim \texttt{Beta} $,
$$ X\vert p \sim \texttt{Binomial}(n,p) $$That is, the data conditioned on $p$, is binomial distributed. Analogously, the multinomial distribution and the Dirichlet distribution also form such a conjugate pair with multinomial parameter $p\sim \texttt{Dirichlet} $,
$$ X\vert p \sim \texttt{multinomial}(n,p) $$For this reason, the Dirichlet-multinomial distribution is popular in machine learning text processing because non-zero probabilities can be assigned to words not specifically contained in specific documents, which helps generalization performance.
Negative Binomial Distribution¶
The negative binomial
distribution is used to characterize the number
of trials until a specified
number of failures ($r$) occurs. For
example, suppose 1 indicates failure
and 0 indicates success. Then
the negative binomial distribution characterizes
the probability of a
k=6 long sequence that has two (r=2) failures, with the
sequence
terminating in a failure (e.g., 001001) with
$\mathbb{P}(1)=1/3$.
The length of the sequence is 6, so for the
negative binomial distribution,
$\mathbb{P}(6-2)=\frac{80}{729}$.
The probability mass function is the following:
$$ \mathbb{P}(k) = \binom{n+k-1}{n-1} p^n (1-p)^k $$where $p$ is the probability of failure. The mean and variance of this distribution is the following:
$$ \mathbb{E}(k) =\frac{n (1-p)}{p} $$$$ \mathbb{V}(k) = \frac{n (1-p)}{p^2} $$The following simulation shows an example sequence generated for the negative binomial distribution.
import random
n=2 # num of failures
p=1/3 # prob of failure
nc = 0 # counter
seq= []
while nc< n:
v,=random.choices([0,1],[1-p,p])
seq.append(v)
nc += (v == 1)
seq,len(seq)
([1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1], 15)
Keep in mind that the negative binomial distribution characterizes the family of such sequences with the specified number of failures.
Negative¶
Multinomial Distribution
The discrete negative multinomial distribution is an
extension of the negative
binomial distribution to account for more than two
possible outcomes. That is,
there are other alteratives whose respective
probabilities sum to one less the
failure probability, $p_{f} = 1-\sum_{k=1}^n
p_i$. For example, a random
sample from this distribution with parameters $n=2$
(number of observed
failures) and with $p_a= \frac{1}{3}, p_b=\frac{1}{2}$ means
that the failure
probability, $p_f=\frac{1}{6}$. Thus, a sample from this
distribution like
$[ 2,9]$ means that 2 of the $a$ objects were observed in
the
sequence, 9 of the $b$ objects were observed, and there were two failure
symbols (say, F) with one of them at the end of the sequence.
The probability mass function is the following:
$$ \mathbb{P}(\mathbf{k})= (n)_{\sum_{i=0}^m k_i} p_f^{n} \prod_{i=1}^m \frac{p_i^{k_i}}{k_i!} $$where $p_f$ is the probability of failure and the other $p_i$ terms are the probabilities of the other alternatives in the sequence. The $(a)_n$ notation is the rising factorial function (e.g., $a_3 = a (a+1)(a+2)$). The mean and variance of this distribution is the following:
$$ \mathbb{E}(\mathbf{k}) =\frac{n}{p_f} \mathbf{p} $$$$ \mathbb{V}(k) = \frac{n}{p_f^2} \mathbf{p} \mathbf{p}^T + \frac{n}{p_f}\diag(\mathbf{p}) $$The following simulation shows the sequences generated for the negative multinomial distribution.
import random
from collections import Counter
n=2 # num of failure items
p=[1/3,1/2] # prob of other non-failure items
items = ['a','b','F'] # F marks failure item
nc = 0 # counter
seq= []
while nc< n:
v,=random.choices(items,p+[1-sum(p)])
seq.append(v)
nc += (v == 'F')
c=Counter(seq)
print(c)
Counter({'a': 3, 'b': 2, 'F': 2})
The values of the Counter dictionary above are the $\mathbf{k}$
vectors in
the probability mass function for the negative multinomial distribution.
Importantly, these are not the probabilities of a particular sequence, but
of a
family of sequences with the same corresponding Counter values.
The
probability mass function implemented in Python is the following,
from scipy.special import factorial
import numpy as np
def negative_multinom_pdf(p,n):
assert len(n) == len(p)
term = [i**j for i,j in zip(p,n)]
num=np.prod(term)*(1-sum(p))*factorial(sum(n))
den = np.prod([factorial(i) for i in n])
return num/den
Evaluating this with the prior Counter result,
negative_multinom_pdf([1/3,1/2],[c['a'],c['b']])
0.015432098765432103