from IPython.display import Image
Image('../../Python_probability_statistics_machine_learning_2E.png',width=200)
%matplotlib inline
import numpy as np
import pandas as pd
from matplotlib.pylab import subplots
from matplotlib.patches import Circle, Rectangle
Survival curves¶
The problem is to estimate the length of time units (e.g.,
subjects,
individuals, components) exist in a cohort over time. For example,
consider the
following data. The rows are the days in a 30-day period and the
columns are the
individual units. For example, these could be five patients who
all receive a
particular treatment on day 0 and then survive (indicated by
1) the next 30
days on not (indicated by 0)
d = pd.DataFrame(index=range(1,8),
columns=['A','B','C','D','E' ],
data=1)
d.loc[3:,'A']=0
d.loc[6:,'B']=0
d.loc[5:,'C']=0
d.loc[4:,'D']=0
d.index.name='day'
d
| A | B | C | D | E | |
|---|---|---|---|---|---|
| day | |||||
| 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 1 | 1 | 1 | 1 |
| 3 | 0 | 1 | 1 | 1 | 1 |
| 4 | 0 | 1 | 1 | 0 | 1 |
| 5 | 0 | 1 | 0 | 0 | 1 |
| 6 | 0 | 0 | 0 | 0 | 1 |
| 7 | 0 | 0 | 0 | 0 | 1 |
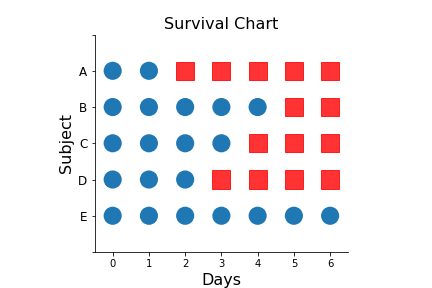
Importantly, survival is a one-way street --- once a subject is dead, then that subject cannot return to the experiment. This is important because survival analysis is also applied to component-failure or other topics where this fact is not so obvious. The following chart shows the survival status of each of the subjects for all seven days. The blue circles indicate that the subject is alive and the red squares indicate death of the subject.
fig,ax =subplots()
_=ax.axis((-0.5,6.5,-1,5))
for ii,jj in zip(*np.where(d.values)):
_=ax.add_patch(Circle((ii,jj),0.25))
for ii,jj in zip(*np.where(d.values==0)):
_=ax.add_patch(Rectangle((ii-0.25,jj-0.25),0.5,0.5,color='red',alpha=.8))
_=ax.set_yticklabels(['','A','B','C','D','E','',''],fontsize=12);
_=ax.invert_yaxis()
_=ax.set_xlabel('Days',fontsize=16)
_=ax.set_ylabel('Subject',fontsize=16)
_=ax.set_title('Survival Chart',fontsize=16)
_=ax.spines['right'].set_visible(0)
_=ax.spines['top'].set_visible(0)
ax.set_aspect(1)
fig.savefig('fig-statistics/survival_analysis_001a.png')
The red squares indicate a dead subject, and the blue a living subject.
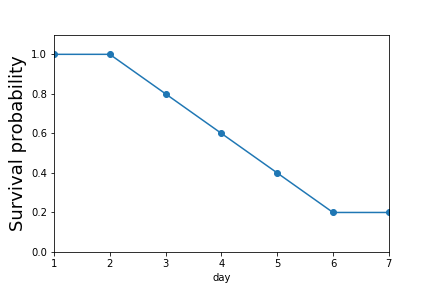
fig,axs=subplots(5,1,sharex=True,sharey=True)
fig.set_size_inches((10,6))
for i,j in enumerate(d.columns):
_=d[j].plot(ax=axs[i],marker='o')
_=axs[i].axis(ymax=1.1,ymin=-.1)
_=axs[i].set_ylabel(j)
fig,ax=subplots()
_=(d.sum(axis=1)/d.shape[1]).plot(ax=ax,marker='o')
_=ax.set_ylabel('Survival probability',fontsize=18)
_=ax.axis(ymin=0,ymax=1.1)
fig.savefig('fig-statistics/survival_analysis_001.png')
The survival probability decreases by day.
There is another important recursive perspective on this calculation. Imagine there is a life raft containing $[A,B,C,D,E]$. Everyone survives until day two when \emph{A} dies. This leaves four in the life raft $[B,C,D,E]$. Thus, from the perspective of day one, the survival probability is the probability of surviving just up until day two and then surviving day two, $\mathbb{P}_S(t\ge 2) =\mathbb{P}(t\notin [0,2)\vert t<2)\mathbb{P}_S(t=2)=(1)(4/5)=4/5$. In words, this means that surviving past the second day is the product of surviving the second day itself and not having a death up to that point (i.e., surviving up to that point). Using this recursive approach, the survival probability for the third day is $\mathbb{P}_S(t\ge 3) =\mathbb{P}_S(t> 3)\mathbb{P}_S(t=3)=(4/5)(3/4)=3/5$. Recall that just before the third day, the life raft contains $[B,C,D,E]$ and on the third day we have $[B,C,E]$. Thus, from the perspective of just before the third day there are four survivors in the raft and on the third day there are three $3/4$. Using this recursive argument generates the same plot and comes in handy with censoring.
Censoring and truncation¶
Censoring occurs when a subject leaves (right censoring) or enters (left censoring) the study. There are two general types of right censoring. The so-called Type I right censoring is when a subject randomly drops out of the study. This random drop-out is another statistical effect that has to be accounted for in estimating survival. Type II right censoring occurs when the study is terminated when enough specific random events occur.
Likewise, left censoring occurs when a subject enters the study prior to a certain date, but exactly when this happened is unknown. This happens in study designs involving two separate studies stages. For example, a subject might enroll in the first selection process but be ineligible for the second process. Specifically, suppose a study concerns drug use and certain subjects have used the drug before the study but are unable to report exactly when. These subjects are left censored. Left truncation (a.k.a. staggered entry, delayed entry) is similar except the date of entry is known. For example, a subject that starts taking a drug after being initially left out of the study.
Right censoring is the most common so let's consider an example. Let's estimate the survival function given the following survival times in days:
$$ \{ 1, 2,3^+,4,5,6^+,7,8 \} $$where the censored survival times are indicated by the plus symbol. As before, the survival time at the $0^{th}$ day is $8/8=1$, the first day is $7/8$, the second day = $(7/8)(6/7)$. Now, we come to the first right censored entry. The survival time for the third day is $(7/8)(6/7)(5/5) = (7/8)(6/7)$. Thus, the subject who dropped out is not considered dead and cannot be counted as such but is considered just absent as far as the functional estimation of the probabilities goes. Continuing for the fourth day, we have $(7/8)(6/7)(5/5)(4/5)$, the fifth day, $(7/8)(6/7)(5/5)(4/5)(3/4)$, the sixth (right censored) day $(7/8)(6/7)(5/5)(4/5)(3/4)(2/2)$, and so on. We can summarize this in the following table:
Hazard functions and their¶
properties
Generally, the survival function is a continuous function of time $S(t) = \mathbb{P}(T>t)$ where $T$ is the event time (e.g., time of death). Note that the cumulative density function, $F(t)=\mathbb{P}(T\le t)=1-S(t)$ and $f(t)=\frac{dF(t)}{dt}$ is the usual probability density function. The so-called hazard function is the instantaneous rate of failure at time $t$,
$$ h(t) = \frac{f(t)}{S(t)} = \lim_{\Delta t \rightarrow 0}\frac{\mathbb{P}(T \in (t,t+\Delta t]|T\ge t)}{\Delta t} $$Note that is a continuous-limit version of the calculation we performed above. In words, it says given the event time $T\ge t$ (subject has survived up to $t$), what is the probability of the event occurring in the differential interval $\Delta t$ for a vanishingly small $\Delta t$. Note that this is not the usual derivative-slope from calculus because there is no difference term in the numerator. The hazard function is also called the force of mortality, intensity rate, or the instantaneous risk. Informally, you can think of the hazard function as encapsulating the two issues we are most concerned about: deaths and the population at risk for those deaths. Loosely speaking, the probability density function in the numerator represents the probability of a death occurring in a small differential interval. However, we are not particularly interested in unqualified deaths, but only deaths that can happen to a specific at-risk population. Returning to our lifeboat analogy, suppose there are 1000 people in the lifeboat and the probability of anybody falling off the lifeboat is 1/1000. Two things are happening here: (1) the probability of the bad event is small and (2) there are a lot of subjects over which to spread the probability of that bad event. This means that the hazard rate for any particular individual is small. On the other hand, if there are only two subjects in the life raft and the probability of falling off is 3/4, then the hazard rate is high because not only is the unfortunate event probable, the risk of that unfortunate event is shared by only two subjects.
It is a mathematical fact that,
$$ h(t) = \frac{-d \log S(t)}{dt} $$This leads to the following interpretation
$$ S(t) = \exp\left( -\int_0^t h(u)du\right) := \exp(-H(t)) $$where $H(t)$ is the cumulative hazard function. Note that $H(t)=-\log S(t)$. Consider a subject whose survival time is 5 years. For this subject to have died at the fifth year, it had to be alive during the fourth year. Thus, the hazard at 5 years is the failure rate per-year, conditioned on the fact that the subject survived until the fourth year. Note that this is not the same as the unconditional failure rate per year at the fifth year, because the unconditional rate applies to all units at time zero and does not use information about survival up to that point gleaned from the other units. Thus, the hazard function can be thought of as the point-wise unconditional probability of experiencing the event, scaled by the fraction of survivors up to that point.
Example¶
To get a sense of this, let's consider the example where the probability density function is exponential with parameter $\lambda$, $f(t)=\lambda \exp(-t\lambda),\; \forall t>0$. This makes $S(t) = 1- F(t) = \exp(-t\lambda)$ and then the hazard function becomes $h(t)=\lambda$, namely a constant. To see this, recall that the exponential distribution is the only continuous distribution that has no memory:
$$ \mathbb{P}(X\le u+t \vert X>u) = 1-\exp(-\lambda t) = \mathbb{P}(X\le t) $$This means no matter how long we have been waiting for a death to occur, the probability of a death from that point onward is the same - thus the hazard function is a constant.
Expectations¶
Given all these definitions, it is an exercise in integration by parts to show that the expected life remaining is the following:
$$ \mathbb{E}(T) = \int_0^\infty S(u) du $$This is equivalent to the following:
$$ \mathbb{E}(T \big\vert t=0) = \int_0^\infty S(u) du $$and we can likewise express the expected remaining life at $t$ as the following,
$$ \mathbb{E}(T \big\vert T\ge t) = \frac{\int_t^\infty S(u) du}{S(t)} $$Parametric regression models¶
Because we are interested in how study parameters affect survival, we need a model that can accommodate regression in exogenous (independent) variables ($\mathbf{x}$).
$$ h(t\vert \mathbf{x})= h_o(t)\exp(\mathbf{x}^T \mathbf{\boldsymbol{\beta}}) $$where $\boldsymbol{\beta}$ are the regression coefficients and $h_o(t)$ is the baseline instantaneous hazard function. Because the hazard function is always nonnegative, the the effects of the covariates enter through the exponential function. These kinds of models are called proportional hazard rate models. If the baseline function is a constant ($\lambda$), then this reduces to the exponential regression model given by the following:
$$ h(t\vert \mathbf{x}) = \lambda \exp(\mathbf{x}^T \mathbf{\boldsymbol{\beta}}) $$Cox proportional hazards model¶
The tricky part about the above proportional hazard rate model is the specification of the baseline instantaneous hazard function. In many cases, we are not so interested in the absolute hazard function (or its correctness), but rather a comparison of such hazard functions between two study populations. The Cox model emphasizes this comparison by using a maximum likelihood algorithm for a partial likelihood function. There is a lot to keep track of in this model, so let's try the mechanics first to get a feel for what is going on.
Let $j$ denote the $j^{th}$ failure time, assuming that failure times are sorted in increasing order. The hazard function for subject $i$ at failure time $j$ is $h_i(t_j)$. Using the general proportional hazards model, we have
$$ h_i(t_j) = h_0(t_j)\exp(z_i \beta) := h_0(t_j)\psi_i $$To keep it simple, we have $z_i \in \{0,1\}$ that indicates membership in the experimental group ($z_{i}=1$) or the control group ($z_i=0$). Consider the first failure time, $t_1$ for subject $i$ failing is the hazard function $h_i(t_1)=h_0(t_1)\psi_{i}$. From the definitions, the probability that subject $i$ is the one who fails is the following:
$$ p_1 = \frac{h_{i}(t_1)}{\sum h_k(t_1)}= \frac{h_{0}(t_1)\psi_i}{\sum h_0(t_1) \psi_k} $$where the summation is over all surviving units up to that point. Note that the baseline hazard cancels out and gives the following,
$$ p_1=\frac{\psi_{i}}{\sum_k \psi_k} $$We can keep computing this for the other failure times to obtain
$\{p_1,p_2,\ldots\,p_D\}$. The product of all of these is the partial
likelihood, $L(\psi) = p_1\cdot p_2\cdots p_D$. The next step is to maximize
this partial likelihood (usually logarithm of the partial likelihood) over
$\beta$. There are a lot of numerical issues to keep track of here. Fortunately,
the Python lifelines
module can keep this all straight for us.
Let's see how
this works using the Rossi dataset that is available in
lifelines.
from lifelines.datasets import load_rossi
from lifelines import CoxPHFitter, KaplanMeierFitter
rossi_dataset = load_rossi()
The Rossi dataset dataset concerns prison recidivism. The fin variable
indicates whether or not the subjects received financial assistance upon
discharge from prison.
week: week of first arrest after release, or
censoring time.
arrest: the event indicator, equal to 1 for those arrested
during the period of the study and 0 for those who were not arrested.
fin:
a factor, with levels yes if the individual received financial aid after release from prison, and no if he did not; financial aid was a randomly assigned factor manipulated by the researchers.
age: in years at the time of release.
race: a factor with levels black and other.
wexp: a factor with levels
yes if the individual had full-time work experience prior to incarceration and no if he did not.
mar: a factor with levels married if the individual was
married at the time of release and not married if he was not.
paro: a
factor coded yes if the individual was released on parole and no if he was not.
prio: number of prior convictions.educ: education, a categorical
variable coded numerically, with codes 2 (grade 6 or less), 3 (grades 6 through 9), 4 (grades 10 and 11), 5 (grade 12), or 6 (some post-secondary).
emp1-
emp52: factors coded yes if the individual was employed in the corresponding
week of the study and no otherwise.
rossi_dataset.head()
| week | arrest | fin | age | race | wexp | mar | paro | prio | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 20 | 1 | 0 | 27 | 1 | 0 | 0 | 1 | 3 |
| 1 | 17 | 1 | 0 | 18 | 1 | 0 | 0 | 1 | 8 |
| 2 | 25 | 1 | 0 | 19 | 0 | 1 | 0 | 1 | 13 |
| 3 | 52 | 0 | 1 | 23 | 1 | 1 | 1 | 1 | 1 |
| 4 | 52 | 0 | 0 | 19 | 0 | 1 | 0 | 1 | 3 |
Now, we just have to set up the calculation in lifelines, using the
scikit- learn style. The lifelines module handles the censoring
issues.
cph = CoxPHFitter()
cph.fit(rossi_dataset,
duration_col='week',
event_col='arrest')
cph.print_summary() # access the results using cph.summary
<lifelines.CoxPHFitter: fitted with 432 observations, 318 censored>
duration col = 'week'
event col = 'arrest'
number of subjects = 432
number of events = 114
partial log-likelihood = -658.75
time fit was run = 2019-08-27 19:17:05 UTC
---
coef exp(coef) se(coef) coef lower 95% coef upper 95% exp(coef) lower 95% exp(coef) upper 95%
fin -0.38 0.68 0.19 -0.75 -0.00 0.47 1.00
age -0.06 0.94 0.02 -0.10 -0.01 0.90 0.99
race 0.31 1.37 0.31 -0.29 0.92 0.75 2.50
wexp -0.15 0.86 0.21 -0.57 0.27 0.57 1.30
mar -0.43 0.65 0.38 -1.18 0.31 0.31 1.37
paro -0.08 0.92 0.20 -0.47 0.30 0.63 1.35
prio 0.09 1.10 0.03 0.04 0.15 1.04 1.16
z p -log2(p)
fin -1.98 0.05 4.40
age -2.61 0.01 6.79
race 1.02 0.31 1.70
wexp -0.71 0.48 1.06
mar -1.14 0.26 1.97
paro -0.43 0.66 0.59
prio 3.19 <0.005 9.48
---
Concordance = 0.64
Log-likelihood ratio test = 33.27 on 7 df, -log2(p)=15.37
The values in the summary are plotted in Figure.
This shows the fitted coefficients from the summary table for each covariate.
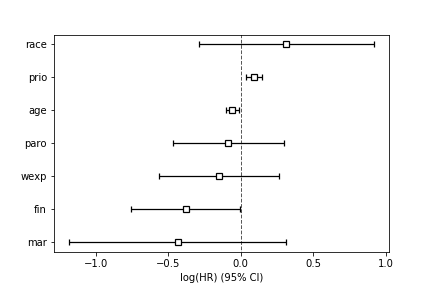
ax=cph.plot();
ax.figure.savefig('fig-statistics/survival_analysis_002.png')
The Cox proportional hazards model object from lifelines allows us to predict
the survival function for an individual with given covariates, assuming that
the
individual just entered the study. For example, for the first individual
(i.e.,
row) in the rossi_dataset, we can use the model to predict the
survival
function for that individual.
cph.predict_survival_function(rossi_dataset.iloc[0,:]).head()
| 0 | |
|---|---|
| T | |
| 1.0 | 0.997616 |
| 2.0 | 0.995230 |
| 3.0 | 0.992848 |
| 4.0 | 0.990468 |
| 5.0 | 0.988085 |
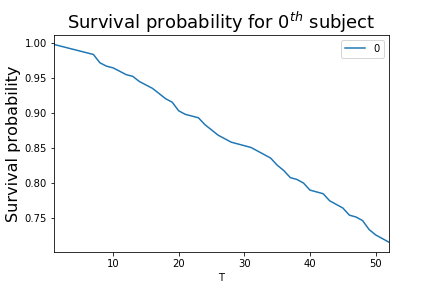
This result is plotted in Figure.
fig,ax =subplots()
_=cph.predict_survival_function(rossi_dataset.iloc[0,:]).plot(ax=ax)
_=ax.set_ylabel('Survival probability',fontsize=16)
_=ax.set_title('Survival probability for $0^{th}$ subject',fontsize=18)
fig.savefig('fig-statistics/survival_analysis_003.png')
The Cox proportional hazards model can predict the survival probability for an individual based on their covariates.