from IPython.display import Image
Image('../../Python_probability_statistics_machine_learning_2E.png',width=200)
We considered Maximum Likelihood Estimation (MLE) and Maximum A-Posteriori (MAP) estimation and in each case we started out with a probability density function of some kind and we further assumed that the samples were identically distributed and independent (iid). The idea behind robust statistics [maronna2006robust] is to construct estimators that can survive the weakening of either or both of these assumptions. More concretely, suppose you have a model that works great except for a few outliers. The temptation is to just ignore the outliers and proceed. Robust estimation methods provide a disciplined way to handle outliers without cherry-picking data that works for your favored model.
The Notion of Location¶
The first notion we need is location, which is a generalization of the idea of central value. Typically, we just use an estimate of the mean for this, but we will see later why this could be a bad idea. The general idea of location satisfies the following requirements Let $X$ be a random variable with distribution $F$, and let $\theta(X)$ be some descriptive measure of $F$. Then $\theta(X)$ is said to be a measure of location if for any constants a and b, we have the following:
$$ \begin{equation} \theta(X+b) = \theta(X) +b \label{_auto1} \tag{1} \end{equation} $$ $$ \begin{equation} \ \theta(-X) = -\theta(X) \label{_auto2} \tag{2} \end{equation} $$ $$ \begin{equation} \ X \ge 0 \Rightarrow \theta(X) \ge 0 \label{_auto3} \tag{3} \end{equation} $$ $$ \begin{equation} \ \theta(a X) = a\theta(X) \label{_auto4} \tag{4} \end{equation} $$The first condition is called location equivariance (or shift-invariance in signal processing lingo). The fourth condition is called scale equivariance, which means that the units that $X$ is measured in should not effect the value of the location estimator. These requirements capture the intuition of centrality of a distribution, or where most of the probability mass is located.
For example, the sample mean estimator is $ \hat{\mu}=\frac{1}{n}\sum X_i $. The first requirement is obviously satisfied as $ \hat{\mu}=\frac{1}{n}\sum (X_i+b) = b + \frac{1}{n}\sum X_i =b+\hat{\mu}$. Let us consider the second requirement:$ \hat{\mu}=\frac{1}{n}\sum -X_i = -\hat{\mu}$. Finally, the last requirement is satisfied with $ \hat{\mu}=\frac{1}{n}\sum a X_i =a \hat{\mu}$.
Robust Estimation and Contamination¶
Now that we have the generalized location of centrality embodied in the location parameter, what can we do with it? Previously, we assumed that our samples were all identically distributed. The key idea is that the samples might be actually coming from a single distribution that is contaminated by another nearby distribution, as in the following:
$$ F(X) = \epsilon G(X) + (1-\epsilon)H(X) $$where $ \epsilon $ randomly toggles between zero and one. This means that our data samples $\lbrace X_i \rbrace$ actually derived from two separate distributions, $ G(X) $ and $ H(X) $. We just don't know how they are mixed together. What we really want is an estimator that captures the location of $ G(X) $ in the face of random intermittent contamination by $ H(X)$. For example, it may be that this contamination is responsible for the outliers in a model that otherwise works well with the dominant $F$ distribution. It can get even worse than that because we don't know that there is only one contaminating $H(X)$ distribution out there. There may be a whole family of distributions that are contaminating $G(X)$. This means that whatever estimators we construct have to be derived from a more generalized family of distributions instead of from a single distribution, as the maximum-likelihood method assumes. This is what makes robust estimation so difficult --- it has to deal with spaces of function distributions instead of parameters from a particular probability distribution.
Generalized Maximum Likelihood Estimators¶
M-estimators are generalized maximum likelihood estimators. Recall that for maximum likelihood, we want to maximize the likelihood function as in the following:
$$ L_{\mu}(x_i) = \prod f_0(x_i-\mu) $$and then to find the estimator $\hat{\mu}$ so that
$$ \hat{\mu} = \arg \max_{\mu} L_{\mu}(x_i) $$So far, everything is the same as our usual maximum-likelihood derivation except for the fact that we don't assume a specific $f_0$ as the distribution of the $\lbrace X_i\rbrace$. Making the definition of
$$ \rho = -\log f_0 $$we obtain the more convenient form of the likelihood product and the optimal $\hat{\mu}$ as
$$ \hat{\mu} = \arg \min_{\mu} \sum \rho(x_i-\mu) $$If $\rho$ is differentiable, then differentiating this with respect to $\mu$ gives
$$ \begin{equation} \sum \psi(x_i-\hat{\mu}) = 0 \label{eq:muhat} \tag{5} \end{equation} $$with $\psi = \rho^\prime$, the first derivative of $\rho$ , and for technical reasons we will assume that $\psi$ is increasing. So far, it looks like we just pushed some definitions around, but the key idea is we want to consider general $\rho$ functions that may not be maximum likelihood estimators for any distribution. Thus, our focus is now on uncovering the nature of $\hat{\mu}$.
Distribution of M-estimates¶
For a given distribution $F$, we define $\mu_0=\mu(F)$ as the solution to the following
$$ \mathbb{E}_F(\psi(x-\mu_0))= 0 $$It is technical to show, but it turns out that $\hat{\mu} \sim \mathcal{N}(\mu_0,\frac{v}{n})$ with
$$ v = \frac{\mathbb{E}_F(\psi(x-\mu_0)^2)}{(\mathbb{E}_F(\psi^\prime(x-\mu_0)))^2} $$Thus, we can say that $\hat{\mu}$ is asymptotically normal with asymptotic value $\mu_0$ and asymptotic variance $v$. This leads to the efficiency ratio which is defined as the following:
$$ \texttt{Eff}(\hat{\mu})= \frac{v_0}{v} $$where $v_0$ is the asymptotic variance of the MLE and measures how near $\hat{\mu}$ is to the optimum. In other words, this provides a sense of how much outlier contamination costs in terms of samples. For example, if for two estimates with asymptotic variances $v_1$ and $v_2$, we have $v_1=3v_2$, then first estimate requires three times as many observations to obtain the same variance as the second. Furthermore, for the sample mean (i.e., $\hat{\mu}=\frac{1}{n} \sum X_i$) with $F=\mathcal{N}$, we have $\rho=x^2/2$ and $\psi=x$ and also $\psi'=1$. Thus, we have $v=\mathbb{V}(x)$. Alternatively, using the sample median as the estimator for the location, we have $v=1/(4 f(\mu_0)^2)$. Thus, if we have $F=\mathcal{N}(0,1)$, for the sample median, we obtain $v={2\pi}/{4} \approx 1.571$. This means that the sample median takes approximately 1.6 times as many samples to obtain the same variance for the location as the sample mean. The sample median is far more immune to the effects of outliers than the sample mean, so this gives a sense of how much this robustness costs in samples.
** M-Estimates as Weighted Means.** One way to think about M-estimates is a weighted means. Operationally, this means that we want weight functions that can circumscribe the influence of the individual data points, but, when taken as a whole, still provide good estimated parameters. Most of the time, we have $\psi(0)=0$ and $\psi'(0)$ exists so that $\psi$ is approximately linear at the origin. Using the following definition:
$$ W(x) = \begin{cases} \psi(x)/x & \text{if} \: x \neq 0 \\\ \psi'(x) & \text{if} \: x =0 \end{cases} $$We can write our Equation 5 as follows:
$$ \begin{equation} \sum W(x_i-\hat{\mu})(x_i-\hat{\mu}) = 0 \label{eq:Wmuhat} \tag{6} \end{equation} $$Solving this for $\hat{\mu} $ yields the following,
$$ \hat{\mu} = \frac{\sum w_{i} x_i}{\sum w_{i}} $$where $w_{i}=W(x_i-\hat{\mu})$. This is not practically useful because the $w_i$ contains $\hat{\mu}$, which is what we are trying to solve for. The question that remains is how to pick the $\psi$ functions. This is still an open question, but the Huber functions are a well-studied choice.
Huber¶
Functions
The family of Huber functions is defined by the following:
$$ \rho_k(x ) = \begin{cases} x^2 & \mbox{if } |x|\leq k \\\ 2 k |x|-k^2 & \mbox{if } |x| > k \end{cases} $$with corresponding derivatives $2\psi_k(x)$ with
$$ \psi_k(x ) = \begin{cases} x & \mbox{if } \: |x| \leq k \\\ \text{sgn}(x)k & \mbox{if } \: |x| > k \end{cases} $$where the limiting cases $k \rightarrow \infty$ and $k \rightarrow 0$ correspond to the mean and median, respectively. To see this, take $\psi_{\infty} = x$ and therefore $W(x) = 1$ and thus the defining Equation 6 results in
$$ \sum_{i=1}^{n} (x_i-\hat{\mu}) = 0 $$and then solving this leads to $\hat{\mu} = \frac{1}{n}\sum x_i$. Note that choosing $k=0$ leads to the sample median, but that is not so straightforward to solve for. Nonetheless, Huber functions provide a way to move between two extremes of estimators for location (namely, the mean vs. the median) with a tunable parameter $k$. The $W$ function corresponding to Huber's $\psi$ is the following:
$$ W_k(x) = \min\Big{\lbrace} 1, \frac{k}{|x|} \Big{\rbrace} $$Figure shows the Huber weight function for $k=2$ with some sample points. The idea is that the computed location, $\hat{\mu}$ is computed from Equation 6 to lie somewhere in the middle of the weight function so that those terms (i.e., insiders) have their values fully reflected in the location estimate. The black circles are the outliers that have their values attenuated by the weight function so that only a fraction of their presence is represented in the location estimate.
This shows the Huber weight function, $W_2(x)$ and some cartoon data points that are insiders or outsiders as far as the robust location estimate is concerned.
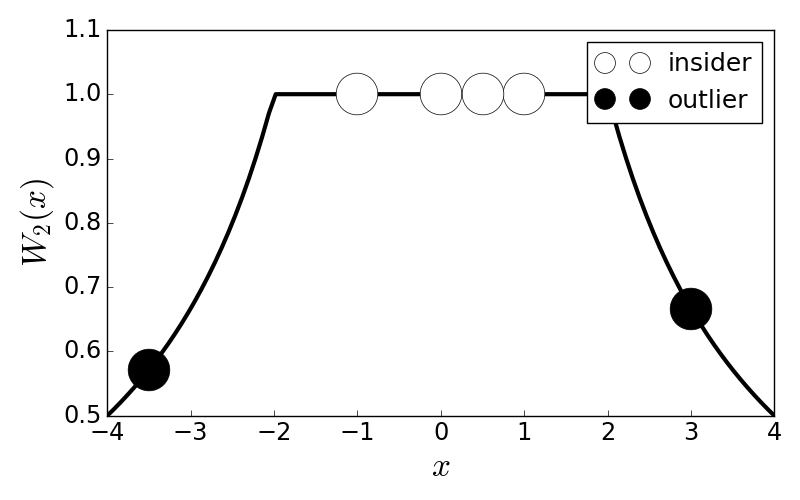
¶
Breakdown Point
So far, our discussion of robustness has been very abstract. A more concrete concept of robustness comes from the breakdown point. In the simplest terms, the breakdown point describes what happens when a single data point in an estimator is changed in the most damaging way possible. For example, suppose we have the sample mean, $\hat{\mu}=\sum x_i/n$, and we take one of the $x_i$ points to be infinite. What happens to this estimator? It also goes infinite. This means that the breakdown point of the estimator is 0%. On the other hand, the median has a breakdown point of 50%, meaning that half of the data for computing the median could go infinite without affecting the median value. The median is a rank statistic that cares more about the relative ranking of the data than the values of the data, which explains its robustness. The simpliest but still formal way to express the breakdown point is to take $n$ data points, $\mathcal{D} = \lbrace (x_i,y_i) \rbrace$. Suppose $T$ is a regression estimator that yields a vector of regression coefficients, $\boldsymbol{\theta}$,
$$ T(\mathcal{D}) = \boldsymbol{\theta} $$Likewise, consider all possible corrupted samples of the data $\mathcal{D}^\prime$. The maximum bias caused by this contamination is the following:
$$ \texttt{bias}_{m} = \sup_{\mathcal{D}^\prime} \Vert T(\mathcal{D^\prime})-T(\mathcal{D}) \Vert $$where the $\sup$ sweeps over all possible sets of $m$ contaminated samples. Using this, the breakdown point is defined as the following:
$$ \epsilon_m = \min \Big\lbrace \frac{m}{n} \colon \texttt{bias}_{m} \rightarrow \infty \Big\rbrace $$For example, in our least-squares regression, even one point at infinity causes an infinite $T$. Thus, for least-squares regression, $\epsilon_m=1/n$. In the limit $n \rightarrow \infty$, we have $\epsilon_m \rightarrow 0$.
¶
Estimating Scale
In robust statistics, the concept of scale refers to a measure of the dispersion of the data. Usually, we use the estimated standard deviation for this, but this has a terrible breakdown point. Even more troubling, in order to get a good estimate of location, we have to either somehow know the scale ahead of time, or jointly estimate it. None of these methods have easy-to-compute closed form solutions and must be computed numerically.
The most popular method for estimating scale is the median absolute deviation
$$ \texttt{MAD} = \texttt{Med} (\vert \mathbf{x} - \texttt{Med}(\mathbf{x})\vert) $$In words, take the median of the data $\mathbf{x}$ and then subtract that median from the data itself, and then take the median of the absolute value of the result. Another good dispersion estimate is the interquartile range,
$$ \texttt{IQR} = x_{(n-m+1)} - x_{(n)} $$where $m= [n/4]$. The $x_{(n)}$ notation means the $n^{th}$ data element after the data have been sorted. Thus, in this notation, $\texttt{max}(\mathbf{x})=x_{(n)}$. In the case where $x \sim \mathcal{N}(\mu,\sigma^2)$, then $\texttt{MAD}$ and $\texttt{IQR}$ are constant multiples of $\sigma$ such that the normalized $\texttt{MAD}$ is the following,
$$ \texttt{MADN}(x) = \frac{\texttt{MAD} }{0.675} $$The number comes from the inverse CDF of the normal distribution corresponding to the $0.75$ level. Given the complexity of the calculations, jointly estimating both location and scale is a purely numerical matter. Fortunately, the Statsmodels module has many of these ready to use. Let's create some contaminated data in the following code,
import statsmodels.api as sm
import numpy as np
from scipy import stats
data=np.hstack([stats.norm(10,1).rvs(10),
stats.norm(0,1).rvs(100)])
These data correspond to our model of contamination that we started
this
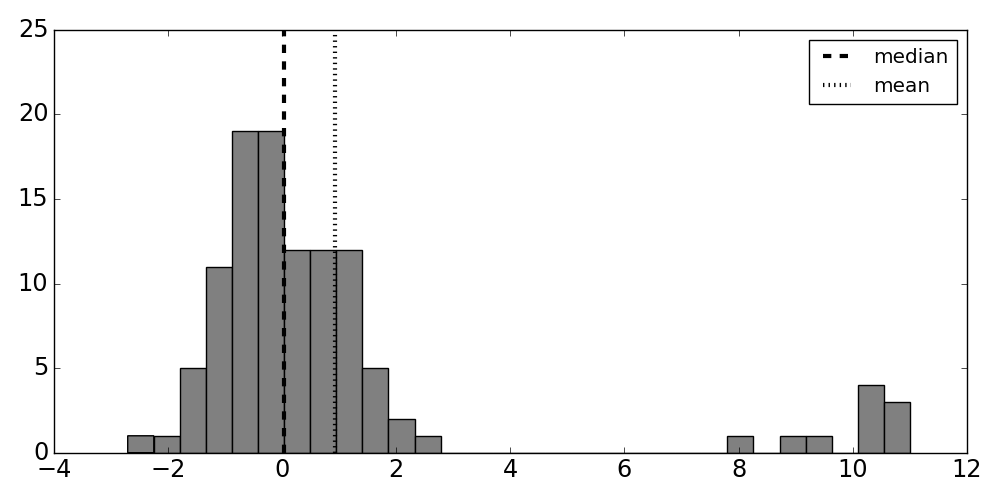
section with. As shown in the histogram in
Figure, there are two normal distributions, one
centered neatly at zero, representing the majority of the samples, and another
coming less regularly from the normal distribution on the right. Notice that
the
group of infrequent samples on the right separates the mean and median
estimates
(vertical dotted and dashed lines). In the absence of the
contaminating
distribution on the right, the standard deviation for this data
should be close
to one. However, the usual non-robust estimate for standard
deviation (np.std)
comes out to approximately three. Using the
$\texttt{MADN}$ estimator
(sm.robust.scale.mad(data)) we obtain approximately
1.25. Thus, the robust
estimate of dispersion is less moved by the presence of
the contaminating
distribution.
Histogram of sample data. Notice that the group of infrequent samples on the right separates the mean and median estimates indicated by the vertical lines.
The generalized maximum likelihood M-estimation extends to joint scale and location estimation using Huber functions. For example,
huber = sm.robust.scale.Huber()
loc,scl=huber(data)
which implements Huber's proposal two method of joint estimation of
location
and scale. This kind of estimation is the key ingredient to robust
regression
methods, many of which are implemented in Statsmodels in
statsmodels.formula.api.rlm. The corresponding documentation has more
information.