from IPython.display import Image
Image('../../Python_probability_statistics_machine_learning_2E.png',width=200)
This chapter takes a geometric view of probability theory and relates it to familiar concepts in linear algebra and geometry. This approach connects your natural geometric intuition to the key abstractions in probability that can help guide your reasoning. This is particularly important in probability because it is easy to be misled. We need a bit of rigor and some intuition to guide us.
In
grade school, you were introduced to the natural numbers (i.e., 1,2,3,..)
and
you learned how to manipulate them by operations like addition,
subtraction, and
multiplication. Later, you were introduced to positive and
negative numbers and
were again taught how to manipulate them. Ultimately, you
were introduced to the
calculus of the real line, and learned how to
differentiate, take limits, and so
on. This progression provided more
abstractions, but also widened the field of
problems you could successfully
tackle. The same is true of probability. One way
to think about probability is
as a new number concept that allows you to tackle
problems that have a special
kind of uncertainty built into them. Thus, the
key idea is that there is some
number, say $x$, with a traveling companion, say,
$f(x)$, and this companion
represents the uncertainties about the value of $x$
as if looking at the number
$x$ through a frosted window. The degree of opacity
of the window is
represented by $f(x)$. If we want to manipulate $x$, then we
have to figure
out what to do with $f(x)$. For example if we want $y= 2 x $,
then we have to
understand how $f(x)$ generates $f(y)$.
Where is the random part? To conceptualize this, we need still another analogy: think about a beehive with the swarm around it representing $f(x)$, and the hive itself, which you can barely see through the swarm, as $x$. The random piece is you don't know which bee in particular is going to sting you! Once this happens the uncertainty evaporates. Up until that happens, all we have is a concept of a swarm (i.e., density of bees) which represents a potentiality of which bee will ultimately sting. In summary, one way to think about probability is as a way of carrying through mathematical reasoning (e.g., adding, subtracting, taking limits) with a notion of potentiality that is so-transformed by these operations.
Understanding Probability Density¶
In order to understand the heart of modern probability, which is built on the Lesbesgue theory of integration, we need to extend the concept of integration from basic calculus. To begin, let us consider the following piecewise function
$$ f(x) = \begin{cases} 1 & \mbox{if } 0 < x \leq 1 \\\ 2 & \mbox{if } 1 < x \leq 2 \\\ 0 & \mbox{otherwise } \end{cases} $$as shown in Figure. In calculus, you learned Riemann integration, which you can apply here as
Simple piecewise-constant function.
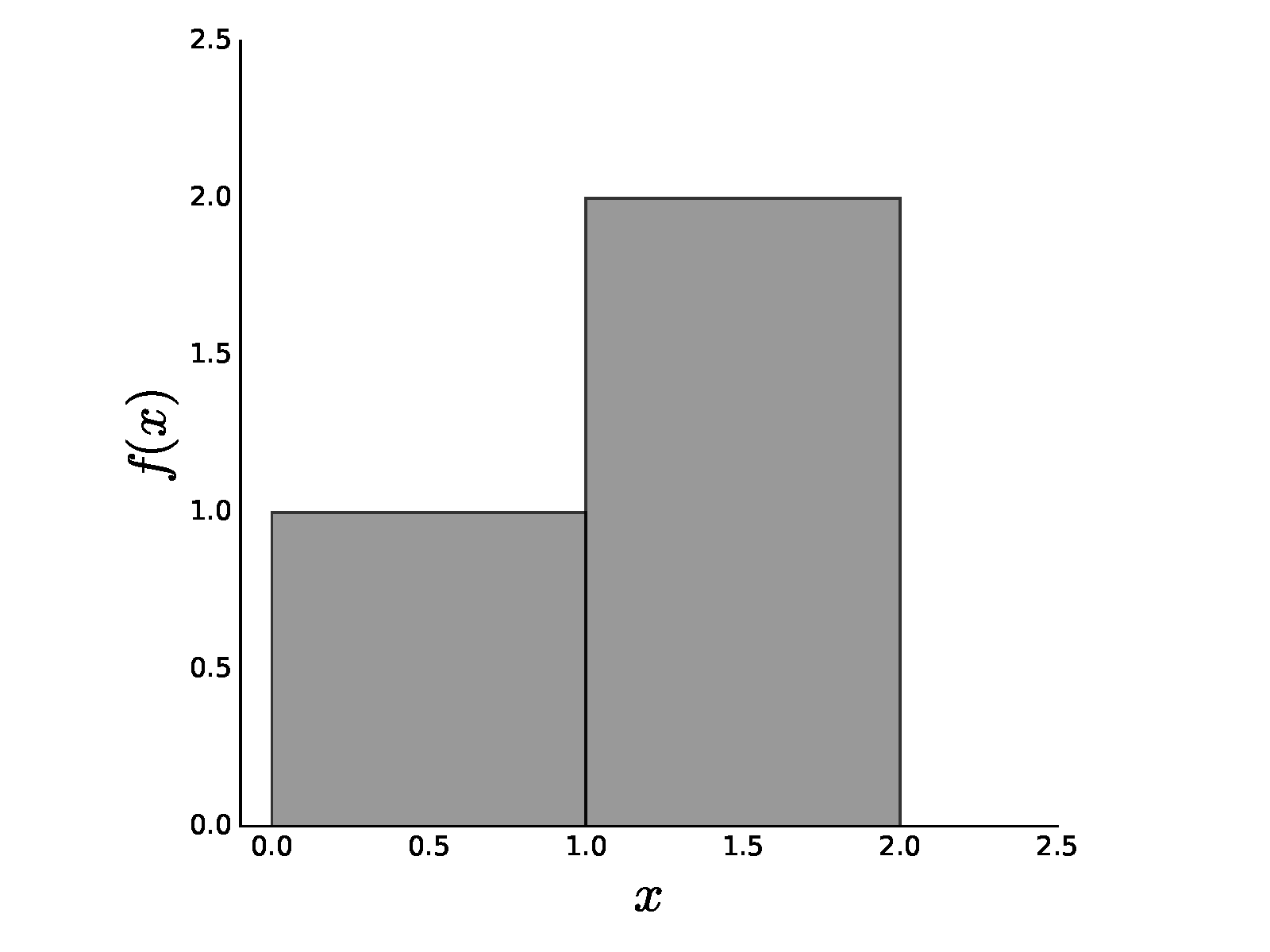 $$
\int_0^2 f(x) dx = 1 + 2 = 3
$$
$$
\int_0^2 f(x) dx = 1 + 2 = 3
$$which has the usual interpretation as the area of the two rectangles that make up $f(x)$. So far, so good.
With Lesbesgue integration, the idea is very
similar except that we
focus on the y-axis instead of moving along the x-axis.
The question
is given $f(x) = 1$, what is the set of $x$ values for which this
is
true? For our example, this is true whenever $x\in (0,1]$. So now we
have a
correspondence between the values of the function (namely, 1
and 2) and the
sets of $x$ values for which this is true, namely,
$\lbrace (0,1] \rbrace$ and
$\lbrace (1,2] \rbrace$, respectively. To
compute the integral, we simply take
the function values (i.e., 1,2)
and some way of measuring the size of the
corresponding interval
(i.e., $\mu$) as in the following:
We have suppressed some of the notation above to emphasize generality. Note that we obtain the same value of the integral as in the Riemann case when $\mu((0,1]) = \mu((1,2]) = 1$. By introducing the $\mu$ function as a way of measuring the intervals above, we have introduced another degree of freedom in our integration. This accommodates many weird functions that are not tractable using the usual Riemann theory, but we refer you to a proper introduction to Lesbesgue integration for further study [jones2001lebesgue]. Nonetheless, the key step in the above discussion is the introduction of the $\mu$ function, which we will encounter again as the so-called probability density function.
Random Variables¶
Most introductions to probability jump straight into random variables and then explain how to compute complicated integrals. The problem with this approach is that it skips over some of the important subtleties that we will now consider. Unfortunately, the term random variable is not very descriptive. A better term is measurable function. To understand why this is a better term, we have to dive into the formal constructions of probability by way of a simple example.
Consider tossing a fair six-sided die. There are only six outcomes possible,
$$ \Omega=\lbrace 1,2,3,4,5,6 \rbrace $$As we know, if the die is fair, then the probability of each outcome is $1/6$. To say this formally, the measure of each set (i.e., $\lbrace 1 \rbrace,\lbrace 2 \rbrace,\ldots,\lbrace 6 \rbrace$) is $\mu(\lbrace 1 \rbrace ) =\mu(\lbrace 2 \rbrace ) \ldots = \mu(\lbrace 6 \rbrace ) = 1/6$. In this case, the $\mu$ function we discussed earlier is the usual probability mass function, denoted by $\mathbb{P}$. The measurable function maps a set into a number on the real line. For example, $ \lbrace 1 \rbrace \mapsto 1 $ is one such function.
Now,
here's where things get interesting. Suppose you were asked to construct a
fair
coin from the fair die. In other words, we want to throw the die and then
record
the outcomes as if we had just tossed a fair coin. How could we do this?
One way
would be to define a measurable function that says if the die comes up
3 or
less, then we declare heads and otherwise declare tails. This has
some
strong intuition behind it, but let's articulate it in terms of formal
theory.
This strategy creates two different non-overlapping sets $\lbrace
1,2,3 \rbrace$
and $\lbrace 4,5,6 \rbrace$. Each set has the same probability
measure,
And the problem is solved. Everytime the die comes up $\lbrace 1,2,3 \rbrace$, we record heads and record tails otherwise.
Is this the only way to construct a fair coin experiment from a fair die? Alternatively, we can define the sets as $\lbrace 1 \rbrace$, $\lbrace 2 \rbrace$, $\lbrace 3,4,5,6 \rbrace$. If we define the corresponding measure for each set as the following
$$ \begin{eqnarray*} \mathbb{P}(\lbrace 1 \rbrace) & = & 1/2 \\\ \mathbb{P}(\lbrace 2 \rbrace) & = & 1/2 \\\ \mathbb{P}(\lbrace 3,4,5,6 \rbrace) & = & 0 \end{eqnarray*} $$then, we have another solution to the fair coin problem. To
implement this,
all we do is ignore every time the die shows 3,4,5,6 and
throw again. This is
wasteful, but it solves the problem. Nonetheless,
we hope you can see how the
interlocking pieces of the theory provide a
framework for carrying the notion of
uncertainty/potentiality from one problem
to the next (e.g., from the fair die
to the fair coin).
Let's consider a slightly more interesting problem where we toss two dice. We assume that each throw is independent, meaning that the outcome of one does not influence the other. What are the sets in this case? They are all pairs of possible outcomes from two throws as shown below,
$$ \Omega = \lbrace (1,1),(1,2),\ldots,(5,6),(6,6) \rbrace $$What are the measures of each of these sets? By virtue of the independence claim, the measure of each is the product of the respective measures of each element. For instance,
$$ \mathbb{P}((1,2)) = \mathbb{P}(\lbrace 1 \rbrace) \mathbb{P}(\lbrace 2 \rbrace) = \frac{1}{6^2} $$With all that established, we can ask the following question: what is the probability that the sum of the dice equals seven? As before, the first thing to do is characterize the measurable function for this as $X:(a,b) \mapsto (a+b)$. Next, we associate all of the $(a,b)$ pairs with their sum. We can create a Python dictionary for this as shown,
d={(i,j):i+j for i in range(1,7) for j in range(1,7)}
The next step is to collect all of the $(a,b)$ pairs that sum to each of the possible values from two to twelve.
from collections import defaultdict
dinv = defaultdict(list)
for i,j in d.items():
dinv[j].append(i)
Programming Tip.
The defaultdict object from the built-in collections
module creates dictionaries with
default values when it encounters a new key.
Otherwise, we would have had to
create default values manually for a regular
dictionary.
For example, dinv[7] contains the following list of pairs that
sum to seven,
dinv[7]
[(1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)]
The next step is to compute the probability measured for each of these items.
Using the independence assumption, this means we have to compute the sum of the
products of the individual item probabilities in dinv. Because we know that
each outcome is equally likely, the probability of every term in the sum equals
$1/36$. Thus, all
we have to do is count the number of items in the
corresponding list for each
key in dinv and divide by 36. For example,
dinv[11] contains [(5, 6), (6, 5)]. The probability of 5+6=6+5=11 is the
probability of this set which
is composed of the sum of the probabilities of the
individual elements
{(5,6),(6,5)}. In this case, we have $\mathbb{P}(11) =
\mathbb{P}(\lbrace
(5,6) \rbrace)+ \mathbb{P}(\lbrace (6,5) \rbrace) = 1/36 +
1/36 = 2/36$.
Repeating this procedure for all the elements, we derive the
probability mass
function as shown below,
X={i:len(j)/36. for i,j in dinv.items()}
print(X)
{2: 0.027777777777777776, 3: 0.05555555555555555, 4: 0.08333333333333333, 5: 0.1111111111111111, 6: 0.1388888888888889, 7: 0.16666666666666666, 8: 0.1388888888888889, 9: 0.1111111111111111, 10: 0.08333333333333333, 11: 0.05555555555555555, 12: 0.027777777777777776}
Programming Tip.
In the preceding code note that 36. is written with
the
trailing decimal mark. This is a good habit to get into
because the default
division operation changed between Python 2.x and
Python 3.x. In Python 2.x
division is integer division by default,
and it is floating-point division in
Python 3.x.
The above example exposes the elements of probability theory that are in play for this simple problem while deliberately suppressing some of the gory technical details. With this framework, we can ask other questions like what is the probability that half the product of three dice will exceed the their sum? We can solve this using the same method as in the following. First, let's create the first mapping,
d={(i,j,k):((i*j*k)/2>i+j+k) for i in range(1,7)
for j in range(1,7)
for k in range(1,7)}
The keys of this dictionary are the triples and the values are the logical values of whether or not half the product of three dice exceeds their sum. Now, we do the inverse mapping to collect the corresponding lists,
dinv = defaultdict(list)
for i,j in d.items():
dinv[j].append(i)
Note that dinv contains only two keys, True and False. Again,
because the
dice are independent, the probability of any triple is $1/6^3$.
Finally, we
collect this for each outcome as in the following,
X={i:len(j)/6.0**3 for i,j in dinv.items()}
print(X)
{False: 0.37037037037037035, True: 0.6296296296296297}
Thus, the probability of half the product of three dice exceeding their sum is
136/(6.0**3) = 0.63. The set that is induced by the random variable has only
two elements in it, True and False, with $\mathbb{P}(\mbox{True})=136/216$
and $\mathbb{P}(\mbox{False})=1-136/216$.
As a final example to exercise another layer of generality, let is consider the first problem with the two dice where we want the probability of a seven, but this time one of the dice is no longer fair. The distribution for the unfair die is the following:
$$ \begin{eqnarray*} \mathbb{P}(\lbrace 1\rbrace)=\mathbb{P}(\lbrace 2 \rbrace)=\mathbb{P}(\lbrace 3 \rbrace) = \frac{1}{9} \\\ \mathbb{P}(\lbrace 4\rbrace)=\mathbb{P}(\lbrace 5 \rbrace)=\mathbb{P}(\lbrace 6 \rbrace) = \frac{2}{9} \end{eqnarray*} $$From our earlier work, we know the elements corresponding to the sum of seven are the following:
$$ \lbrace (1,6),(2,5),(3,4),(4,3),(5,2),(6,1) \rbrace $$Because we still have the independence assumption, all we need to change is the probability computation of each of elements. For example, given that the first die is the unfair one, we have
$$ \mathbb{P}((1,6)) = \mathbb{P}(1)\mathbb{P}(6) = \frac{1}{9} \times \frac{1}{6} $$and likewise for $(2,5)$ we have the following:
$$ \mathbb{P}((2,5)) = \mathbb{P}(2)\mathbb{P}(5) = \frac{1}{9} \times \frac{1}{6} $$and so forth. Summing all of these gives the following:
$$ \mathbb{P}_X(7) = \frac{1}{9} \times \frac{1}{6} +\frac{1}{9} \times \frac{1}{6} +\frac{1}{9} \times \frac{1}{6} +\frac{2}{9} \times \frac{1}{6} +\frac{2}{9} \times \frac{1}{6} +\frac{2}{9} \times \frac{1}{6} = \frac{1}{6} $$Let's try computing this using Pandas instead
of Python dictionaries. First, we
construct
a DataFrame object with an index of tuples
consisting of all pairs
of possible dice outcomes.
from pandas import DataFrame
d=DataFrame(index=[(i,j) for i in range(1,7) for j in range(1,7)],
columns=['sm','d1','d2','pd1','pd2','p'])
Now, we can populate the columns that we set up above
where the outcome of the
first die is the d1 column and
the outcome of the second die is d2,
d.d1=[i[0] for i in d.index]
d.d2=[i[1] for i in d.index]
Next, we compute the sum of the dices in the sm
column,
d.sm=list(map(sum,d.index))
With that established, the DataFrame now looks like the following:
d.head(5) # show first five lines
| sm | d1 | d2 | pd1 | pd2 | p | |
|---|---|---|---|---|---|---|
| (1, 1) | 2 | 1 | 1 | NaN | NaN | NaN |
| (1, 2) | 3 | 1 | 2 | NaN | NaN | NaN |
| (1, 3) | 4 | 1 | 3 | NaN | NaN | NaN |
| (1, 4) | 5 | 1 | 4 | NaN | NaN | NaN |
| (1, 5) | 6 | 1 | 5 | NaN | NaN | NaN |
Next, we fill out the probabilities for each face of the
unfair die (d1) and
the fair die (d2),
d.loc[d.d1<=3,'pd1']=1/9.
d.loc[d.d1 > 3,'pd1']=2/9.
d.pd2=1/6.
d.head(10)
| sm | d1 | d2 | pd1 | pd2 | p | |
|---|---|---|---|---|---|---|
| (1, 1) | 2 | 1 | 1 | 0.111111 | 0.166667 | NaN |
| (1, 2) | 3 | 1 | 2 | 0.111111 | 0.166667 | NaN |
| (1, 3) | 4 | 1 | 3 | 0.111111 | 0.166667 | NaN |
| (1, 4) | 5 | 1 | 4 | 0.111111 | 0.166667 | NaN |
| (1, 5) | 6 | 1 | 5 | 0.111111 | 0.166667 | NaN |
| (1, 6) | 7 | 1 | 6 | 0.111111 | 0.166667 | NaN |
| (2, 1) | 3 | 2 | 1 | 0.111111 | 0.166667 | NaN |
| (2, 2) | 4 | 2 | 2 | 0.111111 | 0.166667 | NaN |
| (2, 3) | 5 | 2 | 3 | 0.111111 | 0.166667 | NaN |
| (2, 4) | 6 | 2 | 4 | 0.111111 | 0.166667 | NaN |
Finally, we can compute the joint probabilities for the sum of the shown faces as the following:
d.p = d.pd1 * d.pd2
d.head(5)
| sm | d1 | d2 | pd1 | pd2 | p | |
|---|---|---|---|---|---|---|
| (1, 1) | 2 | 1 | 1 | 0.111111 | 0.166667 | 0.0185185 |
| (1, 2) | 3 | 1 | 2 | 0.111111 | 0.166667 | 0.0185185 |
| (1, 3) | 4 | 1 | 3 | 0.111111 | 0.166667 | 0.0185185 |
| (1, 4) | 5 | 1 | 4 | 0.111111 | 0.166667 | 0.0185185 |
| (1, 5) | 6 | 1 | 5 | 0.111111 | 0.166667 | 0.0185185 |
With all that established, we can compute the
density of all the dice outcomes
by using groupby as in the
following,
d.groupby('sm')['p'].sum()
sm 2 0.018519 3 0.037037 4 0.055556 5 0.092593 6 0.129630 7 0.166667 8 0.148148 9 0.129630 10 0.111111 11 0.074074 12 0.037037 Name: p, dtype: float64
These examples have shown how the theory of probability breaks down sets and measurements of those sets and how these can be combined to develop the probability mass functions for new random variables.
Continuous Random¶
Variables
The same ideas work with continuous variables but managing the sets becomes trickier because the real line, unlike discrete sets, has many limiting properties already built into it that have to be handled carefully. Nonetheless, let's start with an example that should illustrate the analogous ideas. Suppose a random variable $X$ is uniformly distributed on the unit interval. What is the probability that the variable takes on values less than 1/2?
In order to build intuition onto the discrete case, let's go back to our dice-throwing experiment with the fair dice. The sum of the values of the dice is a measurable function,
$$ Y \colon \lbrace 1,2,\dots,6 \rbrace^2 \mapsto \lbrace 2,3,\ldots, 12 \rbrace $$That is, $Y$ is a mapping of the cartesian product of sets to a discrete set of outcomes. In order to compute probabilities of the set of outcomes, we need to derive the probability measure for $Y$, $\mathbb{P}_Y$, from the corresponding probability measures for each die. Our previous discussion went through the mechanics of that. This means that
$$ \mathbb{P}_Y \colon \lbrace 2,3,\ldots,12 \rbrace \mapsto [0,1] $$Note there is a separation between the function definition and where the target items of the function are measured in probability. More bluntly,
$$ Y \colon A \mapsto B $$with,
$$ \mathbb{P}_Y \colon B \mapsto [0,1] $$Thus, to compute $\mathbb{P}_Y$, which is derived from other random variables, we have to express the equivalence classes in $B$ in terms of their progenitor $A$ sets.
The situation for continuous variables follows the same pattern, but with many more deep technicalities that we are going to skip. For the continuous case, the random variable is now,
$$ X \colon \mathbb{R} \mapsto \mathbb{R} $$with corresponding probability measure,
$$ \mathbb{P}_X \colon \mathbb{R} \mapsto [0,1] $$But where are the corresponding sets here? Technically, these are the Borel sets, but we can just think of them as intervals. Returning to our question, what is the probability that a uniformly distributed random variable on the unit interval takes values less than $1/2$? Rephrasing this question according to the framework, we have the following:
$$ X \colon [0,1] \mapsto [0,1] $$with corresponding,
$$ \mathbb{P}_X \colon [0,1] \mapsto [0,1] $$To answer the question, by the definition of the uniform random variable on the unit interval, we compute the following integral,
$$ \mathbb{P}_X([0,1/2]) = \mathbb{P}_X(0 < X < 1/2) = \int_0^{1/2} dx = 1/2 $$where the above integral's $dx$ sweeps through intervals of the $B$-type. The measure of any $dx$ interval (i.e., $A$-type set) is equal to $dx$, by definition of the uniform random variable. To get all the moving parts into one notationally rich integral, we can also write this as,
$$ \mathbb{P}_X(0 < X < 1/2) = \int_0^{ 1/2 } d\mathbb{P}_X(dx) = 1/2 $$Now, let's consider a slightly more complicated and interesting example. As before, suppose we have a uniform random variable, $X$ and let us introduce another random variable defined,
$$ Y = 2 X $$Now, what is the probability that $0 < Y < \frac{1}{2}$?
To express this in
our framework, we write,
with corresponding,
$$ \mathbb{P}_Y \colon [0,2] \mapsto [0,1] $$To answer the question, we need to measure the set $[0,1/2]$, with the probability measure for $Y$, $\mathbb{P}_Y([0,1/2])$. How can we do this? Because $Y$ is derived from the $X$ random variable, as with the fair-dice throwing experiment, we have to create a set of equivalences in the target space (i.e., $B$-type sets) that reflect back on the input space (i.e., $A$-type sets). That is, what is the interval $[0,1/2]$ equivalent to in terms of the $X$ random variable? Because, functionally, $Y=2 X$, then the $B$-type interval $[0,1/2]$ corresponds to the $A$-type interval $[0,1/4]$. From the probability measure of $X$, we compute this with the integral,
$$ \mathbb{P}_Y([0,1/2]) =\mathbb{P}_X([0,1/4])= \int_0^{1/4} dx = 1/4 $$Now, let's up the ante and consider the following random variable,
$$ Y = X^2 $$where now $X$ is still uniformly distributed, but now over the interval $[-1/2,1/2]$. We can express this in our framework as,
$$ Y \colon [-1/2,1/2] \mapsto [0,1/4] $$with corresponding,
$$ \mathbb{P}_Y \colon [0,1/4] \mapsto [0,1] $$What is the $\mathbb{P}_Y(Y < 1/8)$? In other words, what is the measure of the set $B_Y= [0,1/8]$? As before, because $X$ is derived from our uniformly distributed random variable, we have to reflect the $B_Y$ set onto sets of the $A$-type. The thing to recognize is that because $X^2$ is symmetric about zero, all $B_Y$ sets reflect back into two sets. This means that for any set $B_Y$, we have the correspondence $B_Y = A_X^+ \cup A_X^{-}$. So, we have,
$$ B_Y=\Big\lbrace 0<Y<\frac{1}{8}\Big\rbrace=\Big\lbrace 0<X<\frac{1}{\sqrt{8}} \Big\rbrace \bigcup \Big\lbrace -\frac{1}{\sqrt {8}}<X<0 \Big\rbrace $$From this perspective, we have the following solution,
$$ \mathbb{P}_Y(B_Y)=\mathbb{P}(A_X^+) + \mathbb{P}(A_X^{-}) $$Also,
$$ \begin{align*} A_X^+ &= \Big\lbrace 0< X<\frac{1}{\sqrt{8}} \Big\rbrace \\\ A_X^{-} &= \Big\lbrace -\frac{1}{\sqrt {8}} < X<0 \Big\rbrace \end{align*} $$Therefore,
$$ \mathbb{P}_Y(B_Y) = \frac{1}{\sqrt 8} + \frac{1}{\sqrt 8} $$because $\mathbb{P}(A_X^+) =\mathbb{P}(A_X^-) = 1/\sqrt 8$. Let's see if this comes out using the usual transformation of variables method from calculus. Using this method, the density $f_Y(y) = \frac{1}{ \sqrt y} $. Then, we obtain,
$$ \int_0^{\frac{1}{8}} \frac{1}{\sqrt y} dy = \frac{1}{\sqrt 2} $$which is what we got using the sets method. Note that you would favor the calculus method in practice, but it is important to understand the deeper mechanics, because sometimes the usual calculus method fails, as the next problem shows.
Transformation of Variables Beyond Calculus¶
Suppose $X$ and $Y$ are uniformly distributed in the unit interval and we define $Z$ as
$$ Z = \frac{X}{Y-X} $$What is the $f_Z(z)$? If you try this using the usual calculus method, you will fail (try it!). The problem is one of the technical prerequisites for the calculus method is not in force.
The key observation is that $Z \notin (-1,0]$.
If this were
possible, the $X$ and $Y$ would have different signs, which cannot
happen,
given that $X$ and $Y$ are uniformly distributed over $(0,1]$. Now,
let's
consider when $Z>0$. In this case, $Y>X$ because $Z$ cannot be positive
otherwise. For the density function, we are interested in the set
$\lbrace 0
< Z < z \rbrace $. We want to compute
with,
$$ B_1 = \lbrace 0 < Z < z \rbrace $$Now, we have to translate that interval into an interval relevant to $X$ and $Y$. For $0 < Z$, we have $ Y > X$. For $Z < z $, we have $Y > X(1/z+1)$. Putting this together gives
$$ A_1 = \lbrace \max (X,X(1/z+1)) < Y < 1 \rbrace $$Integrating this over $Y$ as follows,
$$ \int_0^1\lbrace\max(X,X(1/z+1))<Y<1 \rbrace dY=\frac{z-X-Xz}{z}\mbox{ where } z > \frac{X}{1-X} $$and integrating this one more time over $X$ gives
$$ \int_0^{\frac{z}{1+z}} \frac{-X+z-Xz}{z} dX = \frac{z}{2(z+1)} \mbox{ where } z > 0 $$Note that this is the computation for the probability itself, not the probability density function. To get that, all we have to do is differentiate the last expression to obtain
$$ f_Z(z) = \frac{1}{(z+1)^2} \mbox{ where } z > 0 $$Now we need to compute this density using the same process for when $z < -1$. We want the interval $ Z < z $ for when $z < -1$. For a fixed $z$, this is equivalent to $ X(1+1/z) < Y$. Because $z$ is negative, this also means that $Y < X$. Under these terms, we have the following integral,
$$ \int_0^1 \lbrace X(1/z+1) <Y< X\rbrace dY = -\frac{X}{z} \mbox{ where } z < -1 $$and integrating this one more time over $X$ gives the following
$$ -\frac{1}{2 z} \mbox{ where } z < -1 $$To get the density for $z<-1$, we differentiate this with respect to $z$ to obtain the following,
$$ f_Z(z) = \frac{1}{2 z^2} \mbox{ where } z < -1 $$Putting this all together, we obtain,
$$ f_Z(z) = \begin{cases} \frac{1}{(z+1)^2} & \mbox{if } z > 0 \\\ \frac{1}{2 z^2} & \mbox{if } z < -1 \\\ 0 & \mbox{otherwise } \end{cases} $$We will leave it as an exercise to show that this integrates out to one.
Independent Random Variables¶
Independence is a standard assumption. Mathematically, the necessary and sufficient condition for independence between two random variables $X$ and $Y$ is the following:
$$ \mathbb{P}(X,Y) = \mathbb{P}(X)\mathbb{P}(Y) $$Two random variables $X$ and $Y$ are uncorrelated if,
$$ \mathbb{E}\left( (X-\overline{X})(Y-\overline{Y}) \right)=0 $$where $\overline{X}=\mathbb{E}(X)$ Note that uncorrelated random variables are sometimes called orthogonal random variables. Uncorrelatedness is a weaker property than independence, however. For example, consider the discrete random variables $X$ and $Y$ uniformly distributed over the set $\lbrace 1,2,3 \rbrace$ where
$$ X = \begin{cases} 1 & \mbox{if } \omega =1 \\\ 0 & \mbox{if } \omega =2 \\\ -1 & \mbox{if } \omega =3 \end{cases} $$and also,
$$ Y = \begin{cases} 0 & \mbox{if } \omega =1 \\\ 1 & \mbox{if } \omega =2 \\\ 0 & \mbox{if } \omega =3 \end{cases} $$Thus, $\mathbb{E}(X)=0$ and $\mathbb{E}(X Y)=0$, so $X$ and $Y$ are uncorrelated. However, we have
$$ \mathbb{P}(X=1,Y=1)=0\neq \mathbb{P}(X=1)\mathbb{P}(Y=1)=\frac{1}{9} $$So, these two random variables are not independent. Thus, uncorrelatedness does not imply independence, generally, but there is the important case of Gaussian random variables for which it does. To see this, consider the probability density function for two zero-mean, unit-variance Gaussian random variables $X$ and $Y$,
$$ f_{X,Y}(x,y) = \frac{e^{\frac{x^2-2 \rho x y+y^2}{2 \left(\rho^2-1\right)}}}{2 \pi \sqrt{1-\rho^2}} $$where $\rho:=\mathbb{E}(X Y)$ is the correlation coefficient. In the uncorrelated case where $\rho=0$, the probability density function factors into the following,
$$ f_{X,Y}(x,y)=\frac{e^{-\frac{1}{2}\left(x^2+y^2\right)}}{2\pi}=\frac{e^{-\frac{x^2}{2}}}{\sqrt{2\pi}}\frac{e^{-\frac{y^2}{2}}}{\sqrt{2\pi}} =f_X(x)f_Y(y) $$which means that $X$ and $Y$ are independent.
Independence and conditional independence are closely related, as in the following:
$$ \mathbb{P}(X,Y\vert Z) =\mathbb{P}(X\vert Z) \mathbb{P}(Y\vert Z) $$which says that $X$ and $Y$ and independent conditioned on $Z$. Conditioning independent random variables can break their independence. For example, consider two independent Bernoulli-distributed random variables, $X_1, X_2\in\lbrace 0,1 \rbrace$. We define $Z=X_1+X_2$. Note that $Z\in \lbrace 0,1,2 \rbrace$. In the case where $Z=1$, we have,
$$ \begin{align*} \mathbb{P}(X_1\vert Z=1) &>0 \\\ \mathbb{P}(X_2\vert Z=1) &>0 \end{align*} $$Even though $X_1,X_2$ are independent, after conditioning on $Z$, we have the following,
$$ \mathbb{P}(X_1=1,X_2=1\vert Z=1)=0\neq \mathbb{P}(X_1=1\vert Z=1)\mathbb{P}(X_2=1\vert Z=1) $$Thus, conditioning on $Z$ breaks the independence of $X_1,X_2$. This also works in the opposite direction --- conditioning can make dependent random variables independent. Define $Z_n=\sum_i^n X_i$ with $X_i$ independent, integer-valued random variables. The $Z_n$ variables are dependent because they stack the same telescoping set of $X_i$ variables. Consider the following,
$$ \begin{equation} \mathbb{P}(Z_1=i,Z_3=j\vert Z_2=k) = \frac{\mathbb{P}(Z_1=i,Z_2=k,Z_3=j)}{\mathbb{P}(Z_2 =k)} \label{_auto1} \tag{1} \end{equation} $$ $$ \begin{equation} \ =\frac{\mathbb{P}(X_1 =i)\mathbb{P}(X_2 =k-i)\mathbb{P}(X_3 =j-k) }{\mathbb{P}(Z_2 =k)} \end{equation} \label{eq:condIndep} \tag{2} $$where the factorization comes from the independence of the $X_i$ variables. Using the definition of conditional probability,
$$ \mathbb{P}(Z_1=i\vert Z_2)=\frac{\mathbb{P}(Z_1=i,Z_2=k)}{\mathbb{P}(Z_2=k)} $$We can continue to expand Equation 2,
$$ \begin{align*} \mathbb{P}(Z_1=i,Z_3=j\vert Z_2=k) &=\mathbb{P}(Z_1 =i\vert Z_2) \frac{\mathbb{P}( X_3 =j-k)\mathbb{P}( Z_2 =k)}{\mathbb{P}( Z_2 =k)}\\\ &=\mathbb{P}(Z_1 =i\vert Z_2)\mathbb{P}(Z_3 =j\vert Z_2) \end{align*} $$where $\mathbb{P}(X_3=j-k)\mathbb{P}(Z_2=k)= \mathbb{P}(Z_3=j,Z_2)$. Thus, we see that dependence between random variables can be broken by conditioning to create conditionally independent random variables. As we have just witnessed, understanding how conditioning influences independence is important and is the main topic of study in Probabilistic Graphical Models, a field with many algorithms and concepts to extract these notions of conditional independence from graph-based representations of random variables.
Classic Broken Rod¶
Example
Let's do one last example to exercise fluency in our methods by considering the following classic problem: given a rod of unit-length, broken independently and randomly at two places, what is the probability that you can assemble the three remaining pieces into a triangle? The first task is to find a representation of a triangle as an easy-to-apply constraint. What we want is something like the following:
$$ \mathbb{P}(\mbox{ triangle exists }) = \int_0^1 \int_0^1 \lbrace \mbox{ triangle exists } \rbrace dX dY $$where $X$ and $Y$ are independent and uniformly distributed in the unit- interval. Heron's formula for the area of the triangle,
$$ \mbox{ area } = \sqrt{(s-a)(s-b)(s-c)s} $$where $s = (a+b+c)/2$ is what we need. The idea is that this yields a valid area only when each of the terms under the square root is greater than or equal to zero. Thus, suppose that we have
$$ \begin{eqnarray*} a & = & X \\\ b & = & Y-X \\\ c & = & 1-Y \end{eqnarray*} $$assuming that $Y>X$. Thus, the criterion for a valid triangle boils down to
$$ \lbrace (s > a) \wedge (s > b) \wedge (s > c) \wedge (X<Y) \rbrace $$After a bit of manipulation, this consolidates into:
$$ \Big\lbrace \frac{1}{2} < Y < 1 \bigwedge \frac{1}{2}(2 Y-1) < X < \frac{1}{2} \Big\rbrace $$which we integrate out by $dX$ first to obtain
$$ \mathbb{P}(\mbox{ triangle exists }) = \int_{0}^1 \int_{0}^1 \Big\lbrace \frac{1}{2} < Y < 1 \bigwedge \frac{1}{2}(2 Y-1) < X < \frac{1}{2} \Big\rbrace dX dY $$$$ \mathbb{P}(\mbox{ triangle exists }) = \int_{\frac{1}{2}}^1 (1-Y) dY $$and then by $dY$ to obtain finally,
$$ \mathbb{P}(\mbox{ triangle exists }) = \frac{1}{8} $$when $Y>X$. By symmetry, we get the same result for $X>Y$. Thus, the final result is the following:
$$ \mathbb{P}(\mbox{ triangle exists }) = \frac{1}{8}+\frac{1}{8} = \frac{1}{4} $$We can quickly check using this result using Python for the case $Y>X$ using the following code:
import numpy as np
x,y = np.random.rand(2,1000) # uniform rv
a,b,c = x,(y-x),1-y # 3 sides
s = (a+b+c)/2
np.mean((s>a) & (s>b) & (s>c) & (y>x)) # approx 1/8=0.125
0.129
Programming Tip.
The chained logical & symbols above tell Numpy that the
logical operation
should be considered element-wise.