Notebook

June 11, 2015¶

Project Status Update¶

Summary¶

Resolved issues in FLASH4 RadTrans routines that had been resulting in either pockets of cold gas or a shutdown in accretion onto the sink particle
These problems were related to the updated radiation diffusion equation

$$ \frac{E_r^{n+1} - E_r^{n}}{\Delta t} - \nabla \cdot \left( D^{n} \nabla E_r^{n+1}\right) + \kappa \rho c \left[\frac{ \rho c_V T^{n}}{\rho c_V T^{n} + 4 \alpha a_R \left(T^{n}\right)^4}\right] E_r^{n+1} = \kappa \rho c a_R \left(T^{n}\right)^4 \left[\frac{\rho c_V T^{n} - 4 \Delta t \nabla \cdot F_*}{\rho c_V T^{n} + 4 \alpha a_R \left(T^{n}\right)^4} \right] $$

The terms in square braces are the "correction factors" that result from the linearization of the temperature update equation. A derivation is given in our code paper (Klassen et al. 2015).

A sign error in the irradiation component, $\nabla \cdot F_*$, of the correction factor for the emission term (right hand side of the above equation) resulted in strong cooling near the sink particle. This was not discovered until recently. I had misinterpreted the cooling as a problem with how FLASH's diffusion solver was handling the correction factors. In comparing to the FLASH user guide, the coupled energy equations were written with an explicit temperature term, that is, the temperature at time index n, whereas we were using a linearized temperature updated to time index n+1. Moreover, the matter-radiation coupling test was failing and, concerned about this, I set the correction factors equal to 1.0 and ran further tests.

Meanwhile, at the FLASH Center at the University of Chicago, Klaus Weide has become convinced that our correction factors are indeed the way to go and should be fully compatible with FLASH's diffusion routines. After closer inspection, I discovered the sign error. Moreover, we are able to run the energy-coupling test without problems, likely because other bugs were tracked down and corrected.

Klaus Weide and Manos Chatzopoulos of the FLASH Center delivered to us a modified unsplit hydro solver that includes the $\lambda$ flux limiter and radiation energy gradients in calculating the diffuse radiation pressure hydro terms.
Under this solver, we were able to run the 1D radiative shock test and get much better agreement on the pre-shock temperature. If you recall, in our code paper, this was our worst test result.
Klaus also created a modified equation of state (EOS) routine that throws out one of the two matter species in FLASH4. If you recall, the original FLD code was written for high-energy-density plasmas and there are two matter species: electrons and ions. The ions carry the momentum and the electrons interact with the radiation field. A separate routine couples the two species together and they exchange energy in a time-dependent way. This was always irritating to us because we are principally concerned with only a single matter species and the HeatExchange module is wasted computation.

Appendix A in Klassen et al. 2015 explains how we forcibly had to equilibrate the two matter species so that we could have a single quasineutral fluid.

With the new EOS, this is a moot point. The "electrons" are now our only matter species. Their mean molecular weight is set with a runtime parameter. The fluid behaves just as we want it to.

Dust evaporation has been added following Section 2.6 in Kuiper et al. 2010

Remaining Issues¶

We linearized the temperature update term:

$$ \left(T^{n+1}\right)^4 = (T^n)^4\left(1+\frac{T^{n+1} - T^n}{T^n}\right)^4 \approx 4\left(T^n\right)^3 T^{n+1} - 3\left(T^n\right)^4. $$

As a result of this choice, when the change in temperature from one time step to the next becomes large, then the higher-order terms dropped from this approximation become important and our temperatures can become inaccurate.
The expansion is a binomial expansion of the form

$$ (1+x)^4 = 1 + 4x + 6x^2 + 4x^3 + x^4, $$

where $$ x = \frac{\Delta T}{T} = \frac{T_{new}-T_{old}}{T_{old}} $$

The reason we keep only the linear term is that we use it to write the temperature update equation:

$$ T^{n+1} = \frac{3 a_R \alpha \left(T^n\right)^4 + \rho c_V T^n + \alpha E_r^{n+1} - \Delta t \nabla \cdot \vec{F}_*}{\rho c_V + 4 a_R \alpha \left(T^n\right)^3}, $$

where $\alpha \equiv \kappa_P^n \rho c \Delta t$.

Keeping higher-order terms would mean a root-solve operation would need to be performed at every cell for every timestep in order to update the temperature.

The second order term, $\mathcal{O}2 = 6(\Delta T/T)^2$, becomes an appreciable fraction (0.1) of the first order term, $\mathcal{O}1 = 4(\Delta T/T)$ for temperature changes as small as 6.7%.
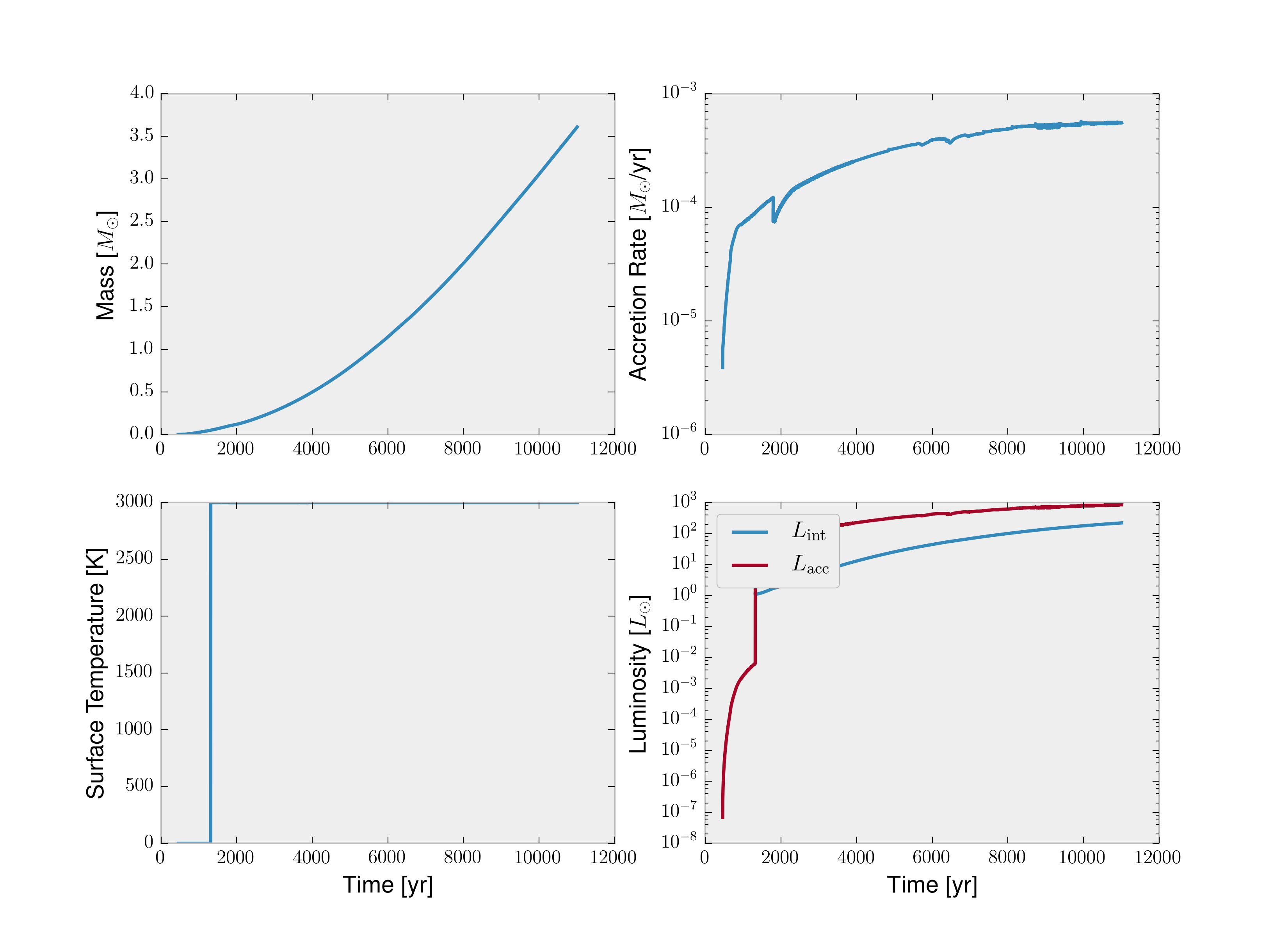
I have modified the FLASH timestep limiter to check for temperature changes that exceed this criterion and reduce the timestep appropriately. What I found was that the timestep was often made unrealistically small. In particular, with strong irradiation by the accreting source, timesteps can be reduced below even $10^6$ seconds.
Some of the latest tests have been run using fixed timesteps above the "safety" criterion, at timestep sizes ranging between $10^7$ and $5 \times 10^7$ seconds.
Under these conditions, we find temperatures in some cells can exceed 10^4 K.

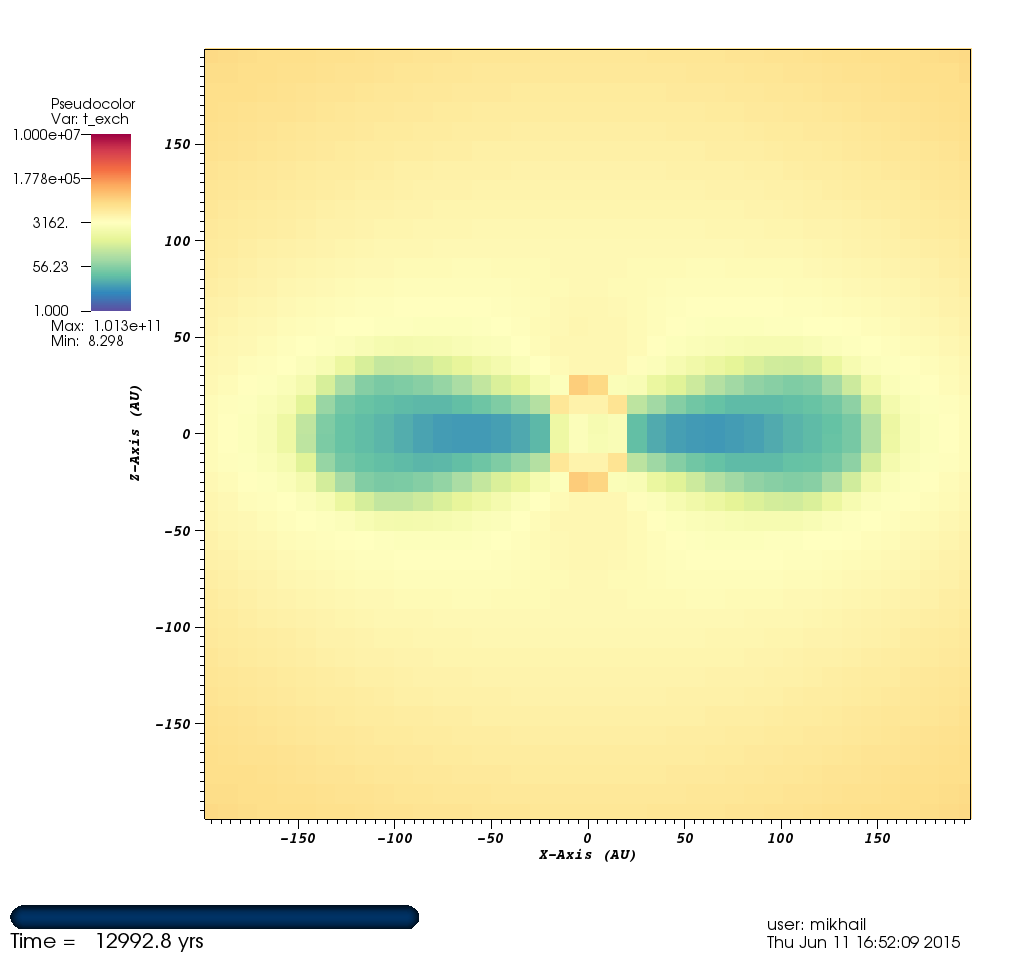
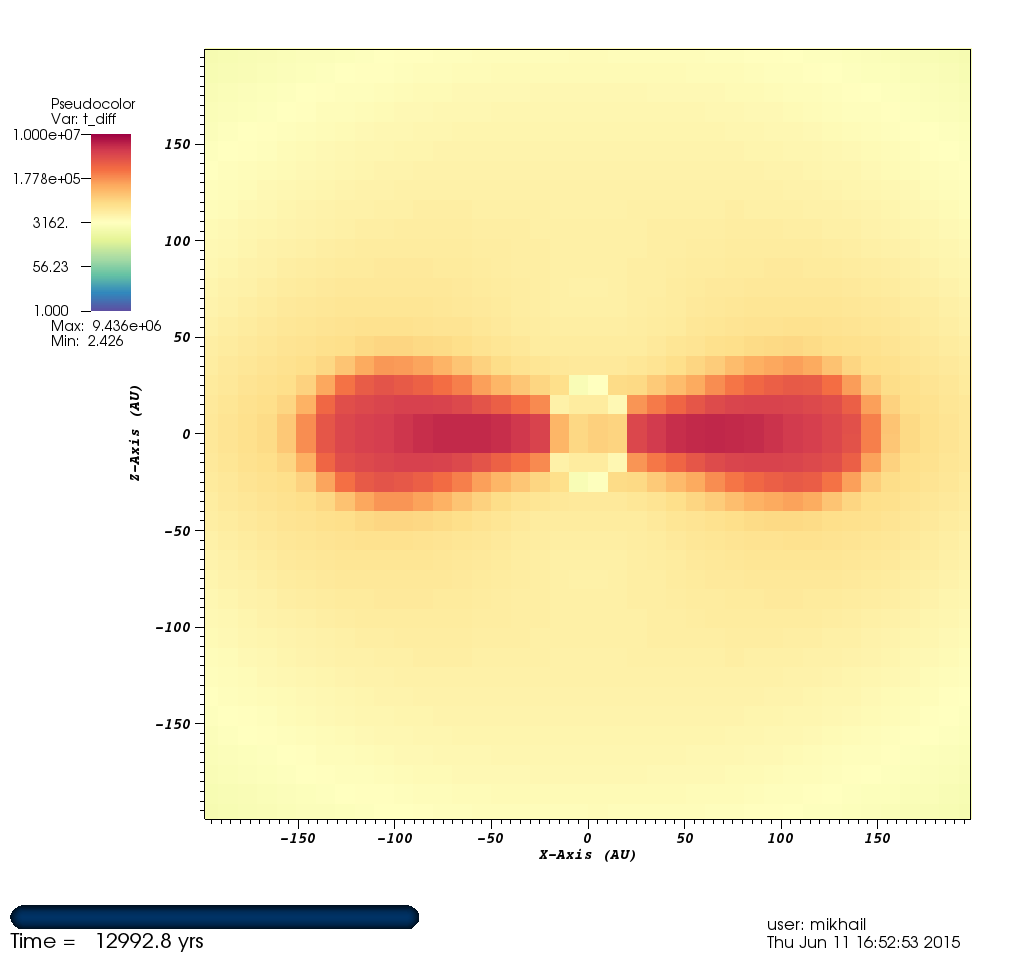
Timescales and subcycling¶

There are several relevant physical timescales:

Matter-Radiation energy exchange (coupling) timescale:

$$ t_{exch} = \frac{1}{\kappa_P \rho c} $$

Diffusion timescale:

$$ t_{diff} = \frac{(\Delta x)^2}{\frac{c}{3.0 \kappa_R \rho}} $$

Sonic flow:

$$ t_{flow} = \frac{\Delta x}{c_s}, $$

where $c_s$ is the sound speed.

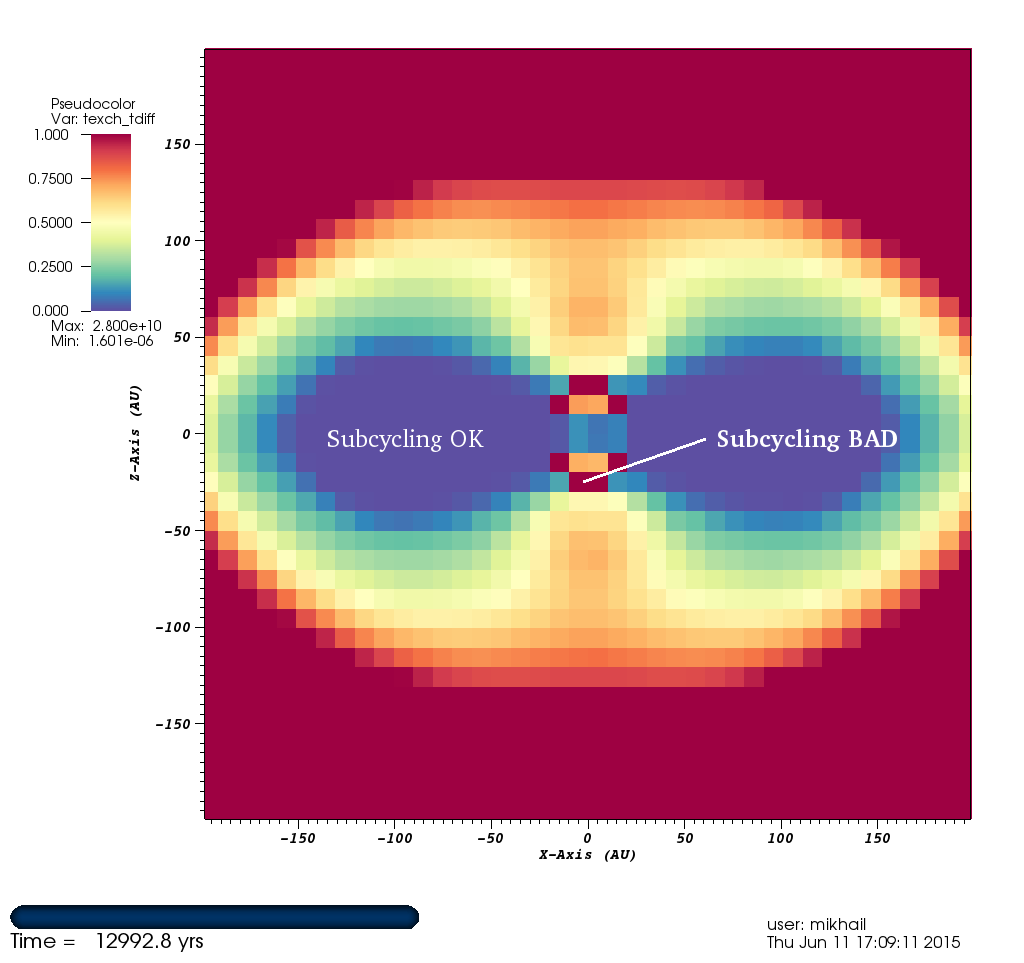
In practice, the first two are the most relevant. In high-density regions, $t_{exch}$ tends to be much shorter than other timescales. In these regions, I have implemented temperature update subcycling. I have FLASH check whether the temperature update will be outside of a "safe" limit for our linearization. Then I check whether $t_{exch}$ is much shorter than the other timescales. Then I calcualate a safe timestep size and repeatedly apply the temperature update equation with the subcycling timestep until either I reach the global timestep or the temperature changes less than 1% between iterations.

This subcycling approach helps partially circumvent the problem of FLASH not having adaptive timestepping (i.e. where different parts of the grid can be updated with different timestep sizes).

The problem is that with dust evaporation, the diffusion timestep can become comparably short relative to the energy coupling timestep. In this regime, it may not be physically accurate to apply subcycling because you are not accounting for radiation energy diffusing into or out of a cell. It is in these cells that we are seeing temperatures exceed $10^4$ K.

Results¶

Figure 1: Density¶

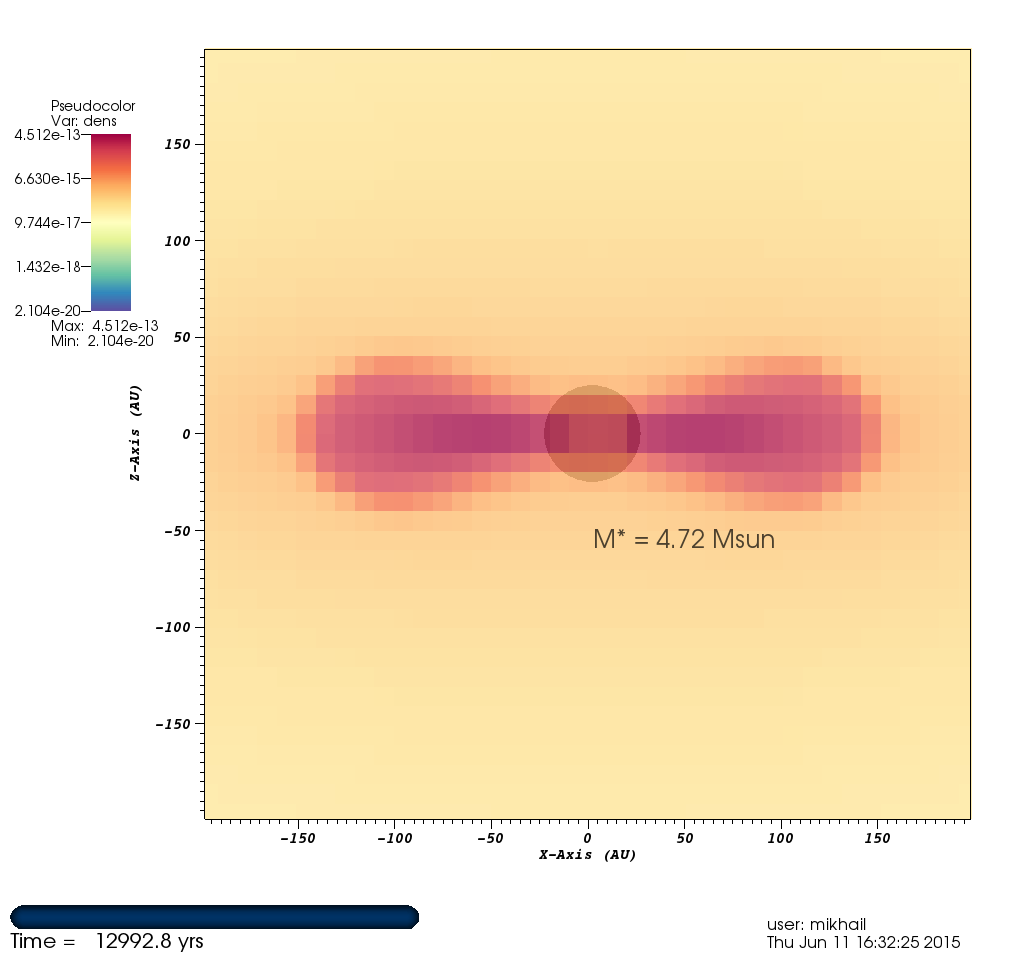
Figure 2: Velocity Structure¶

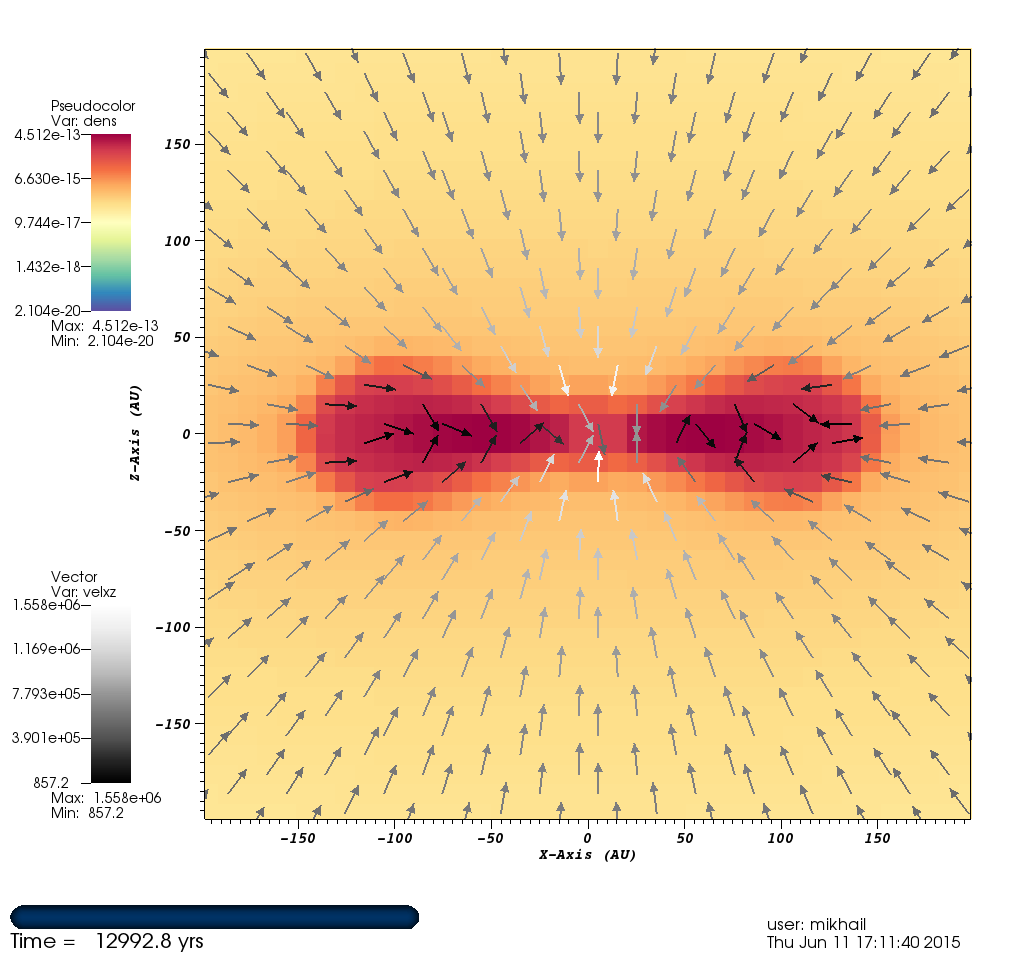
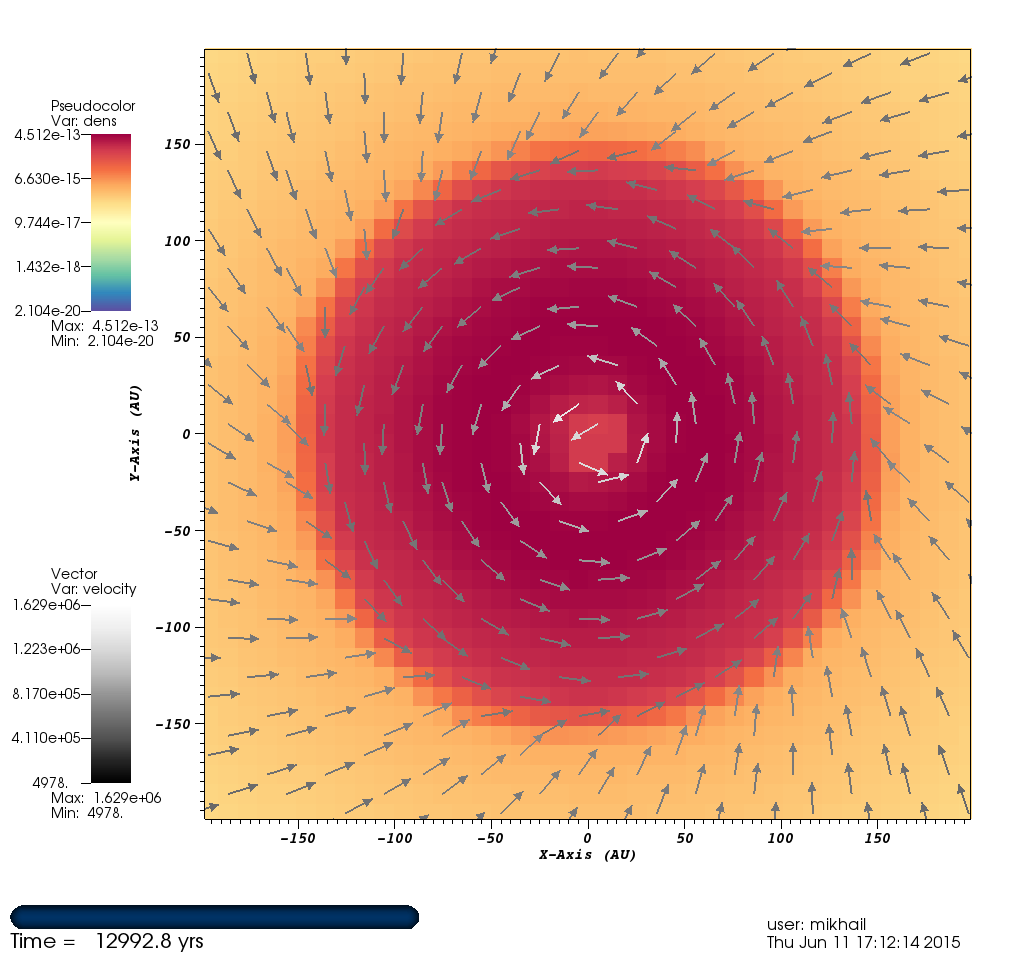
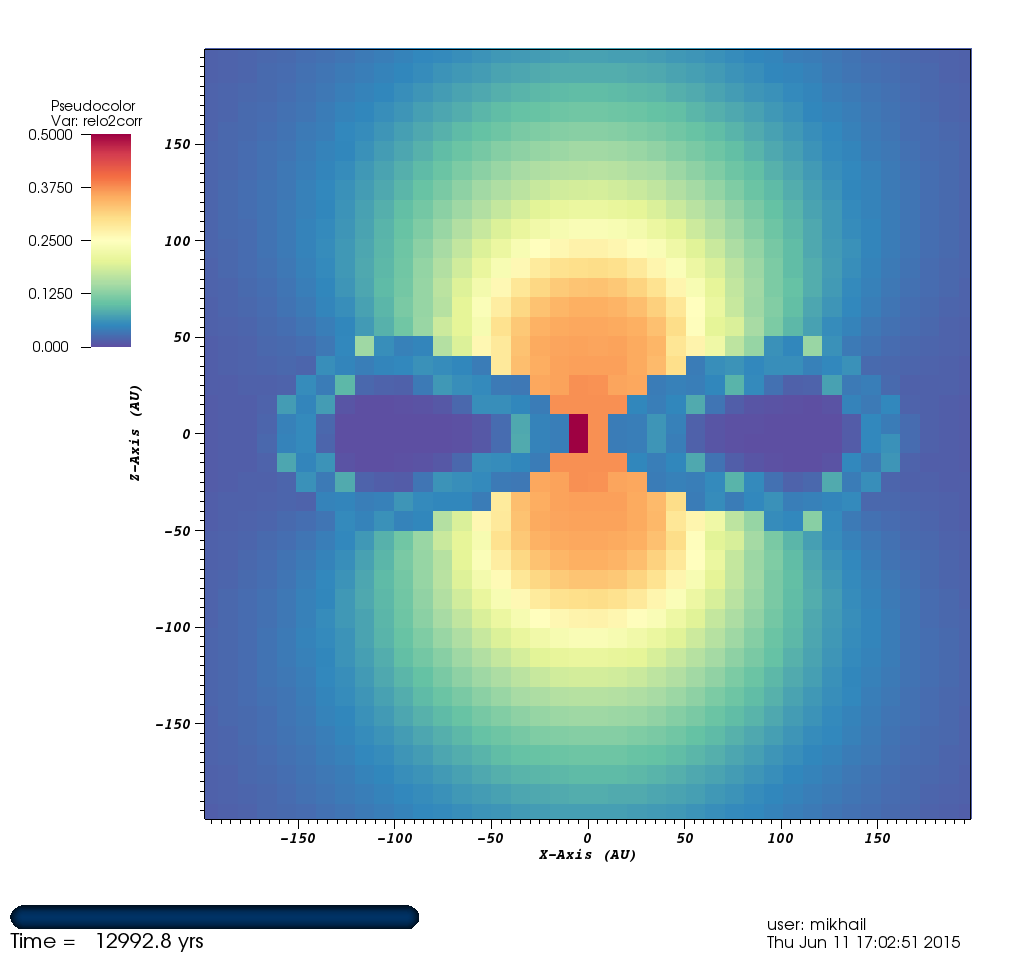
Figure 3: Temperature¶

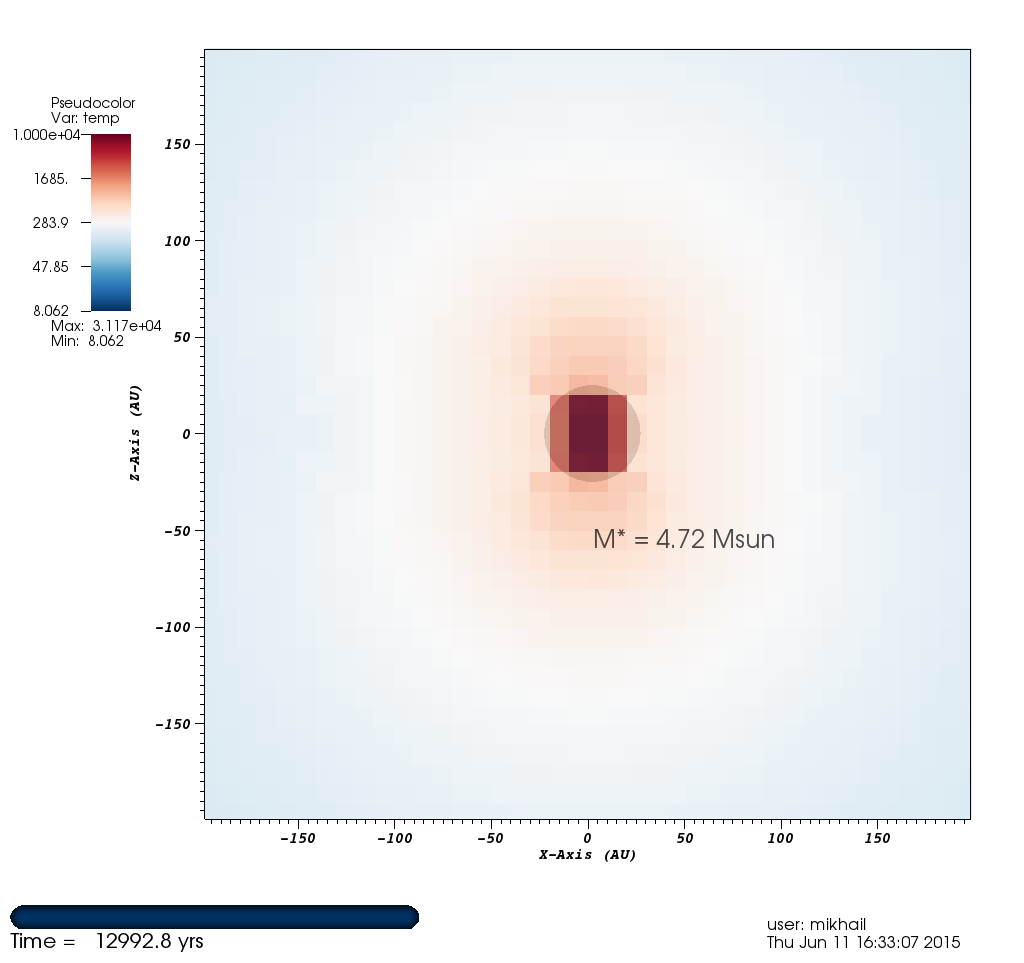
Figure 4: Temperature Face-On View with Velocities¶

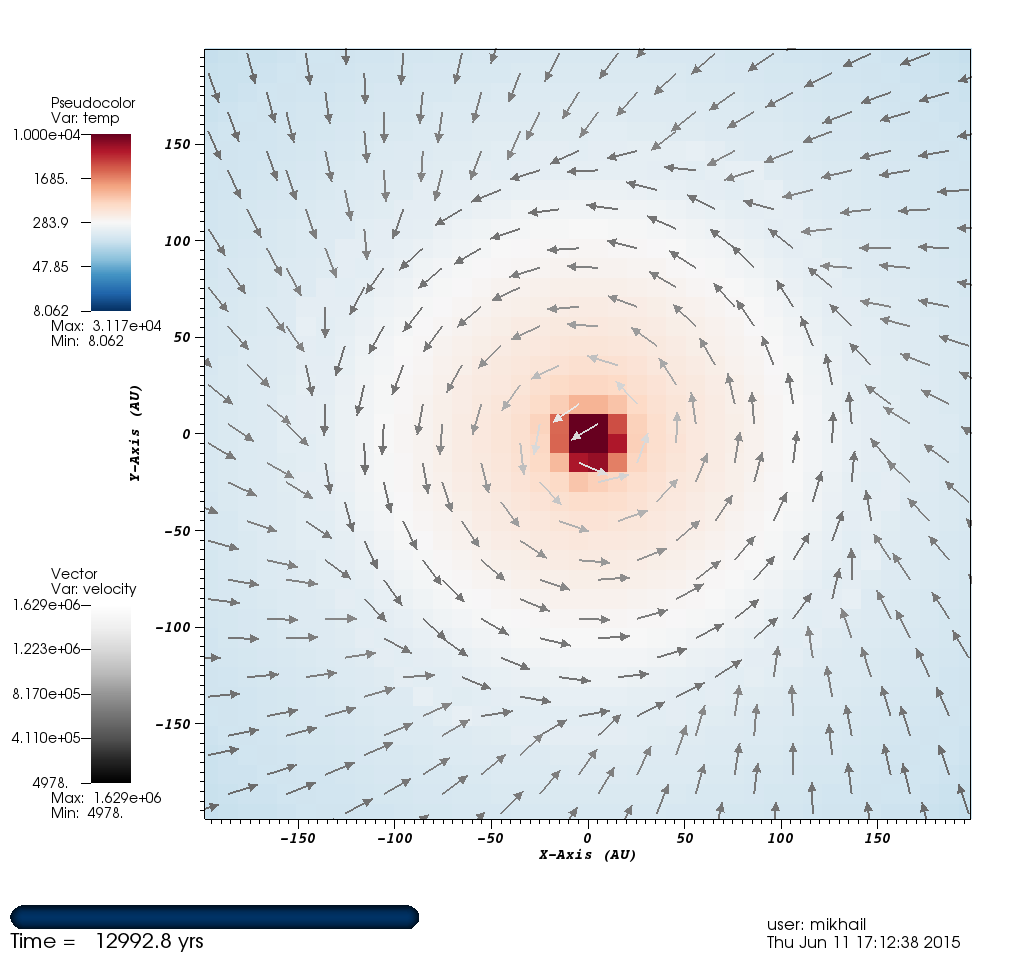
Figure 5: Radial Temperature Profile¶

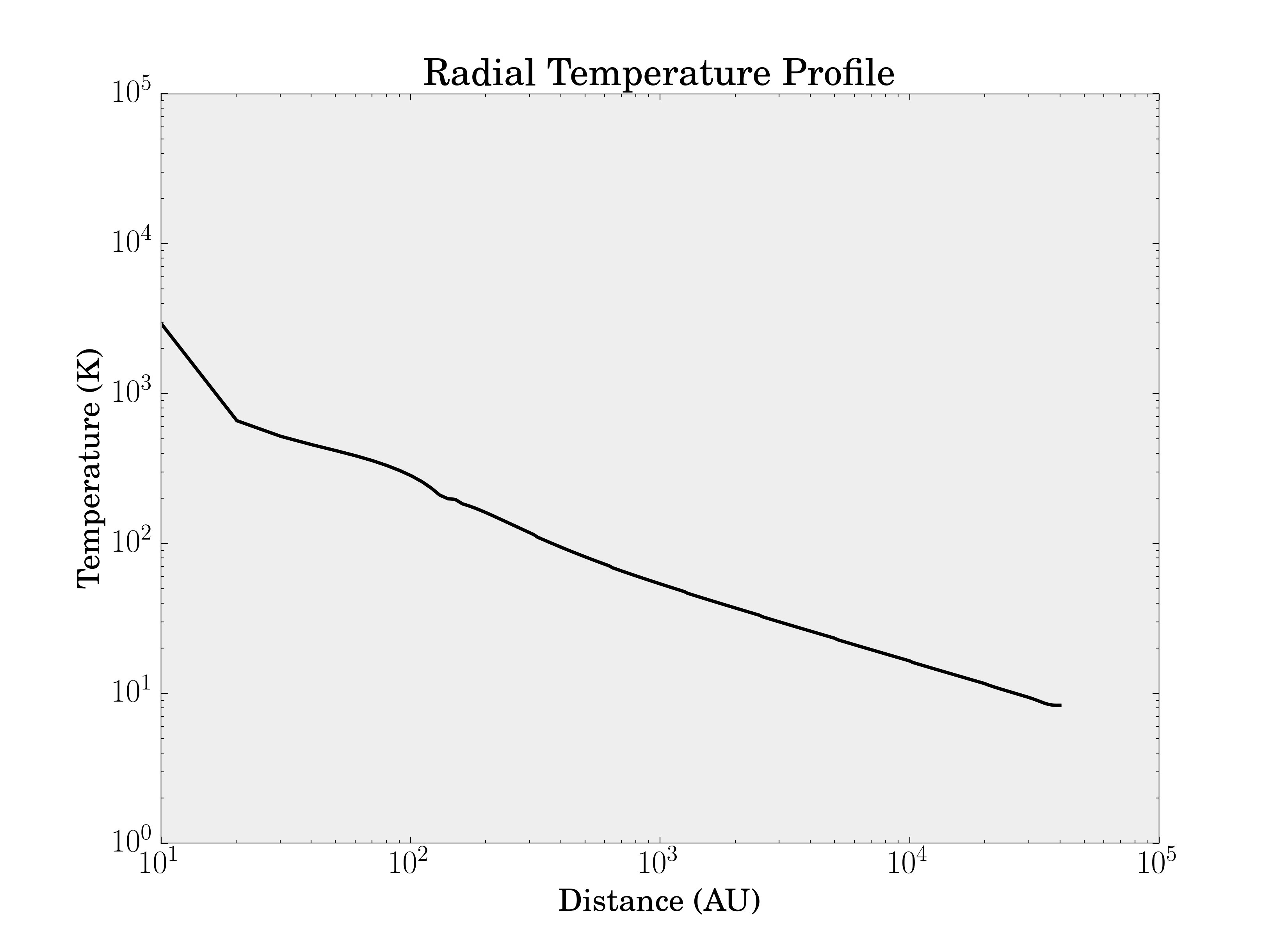
Figure 6: Planck & Rosseland Mean Opacities¶

Shown below are the Planck & Rosseland mean opacities with contours of optical depth $\tau$.

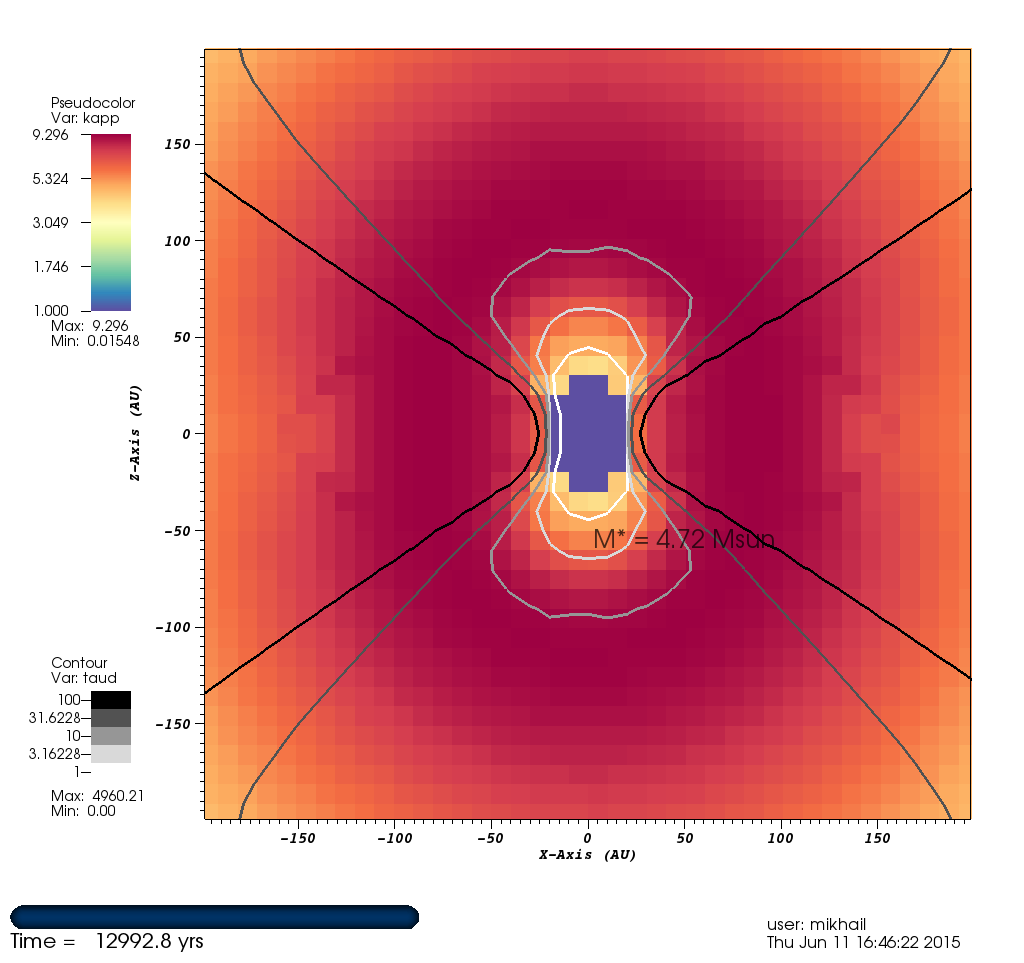
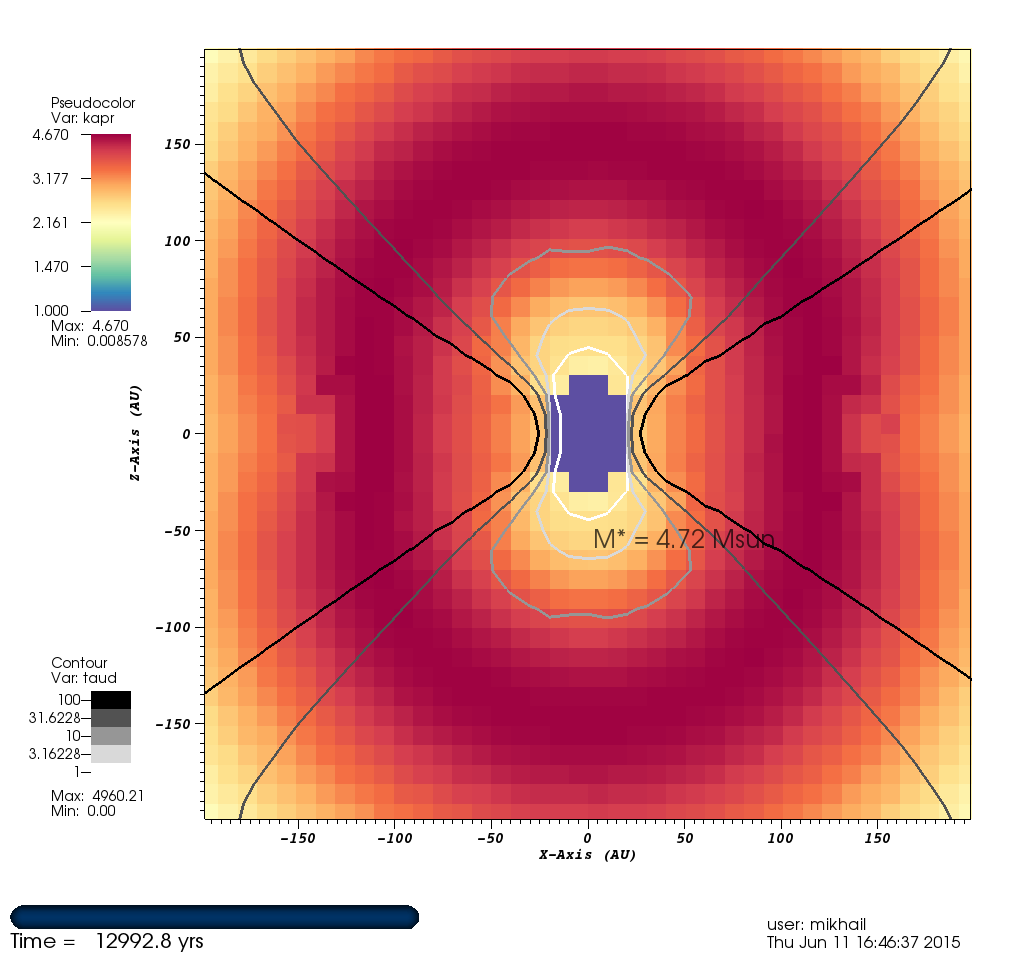
Figure 7: Optical Depth¶

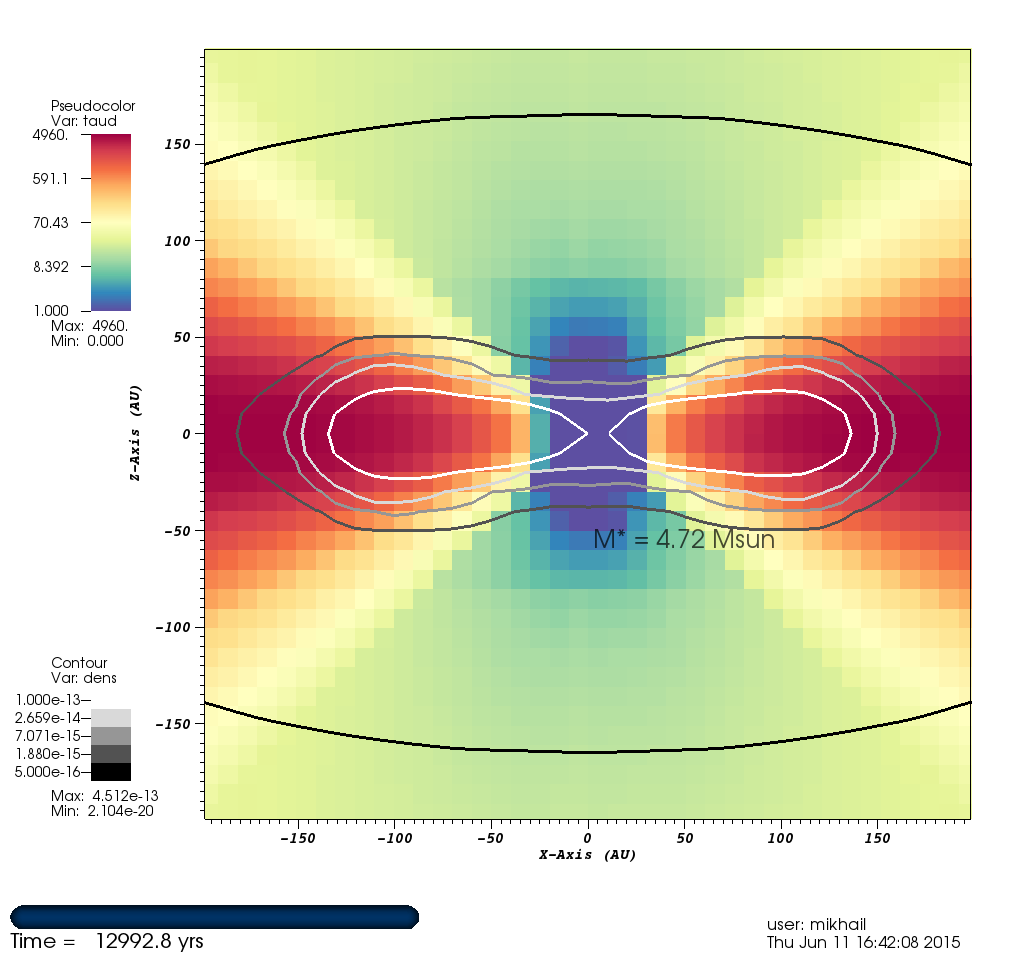The above is with contours of density.

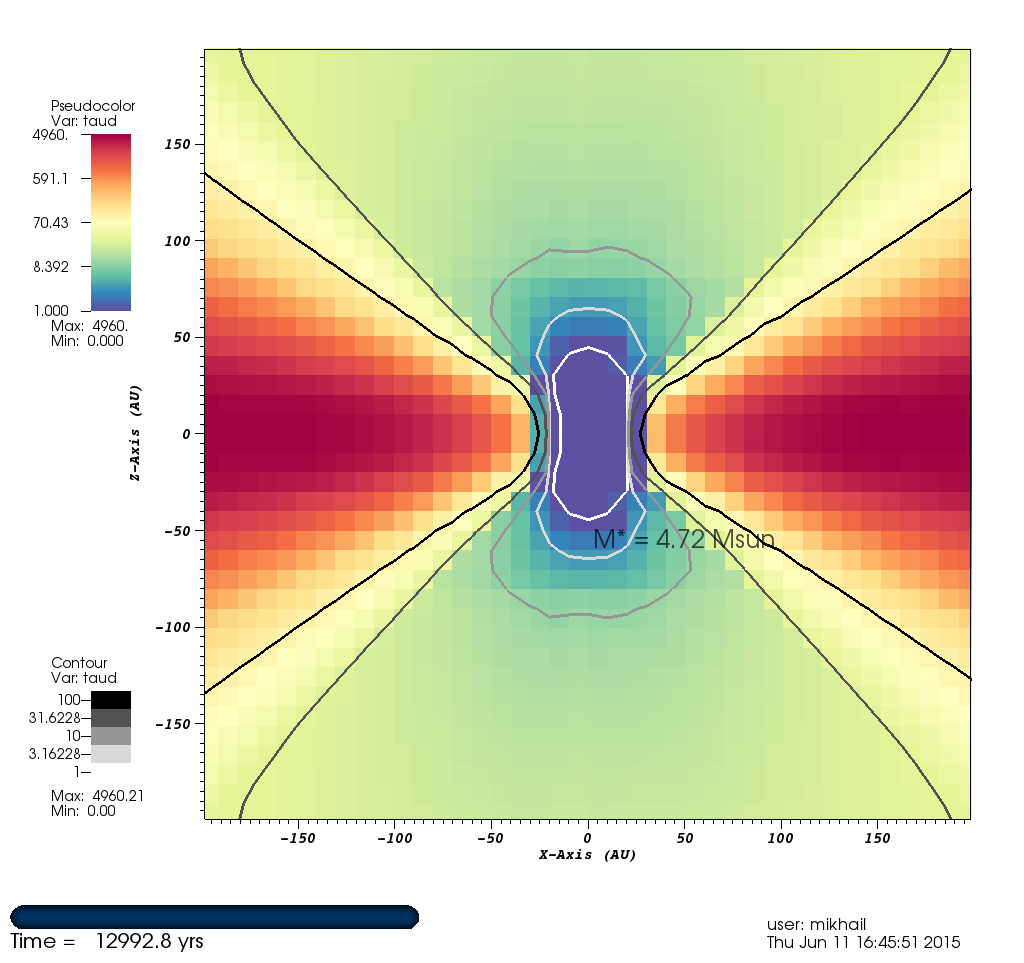This image shows contours of optical depth.

Figure 8: Dust Fraction¶

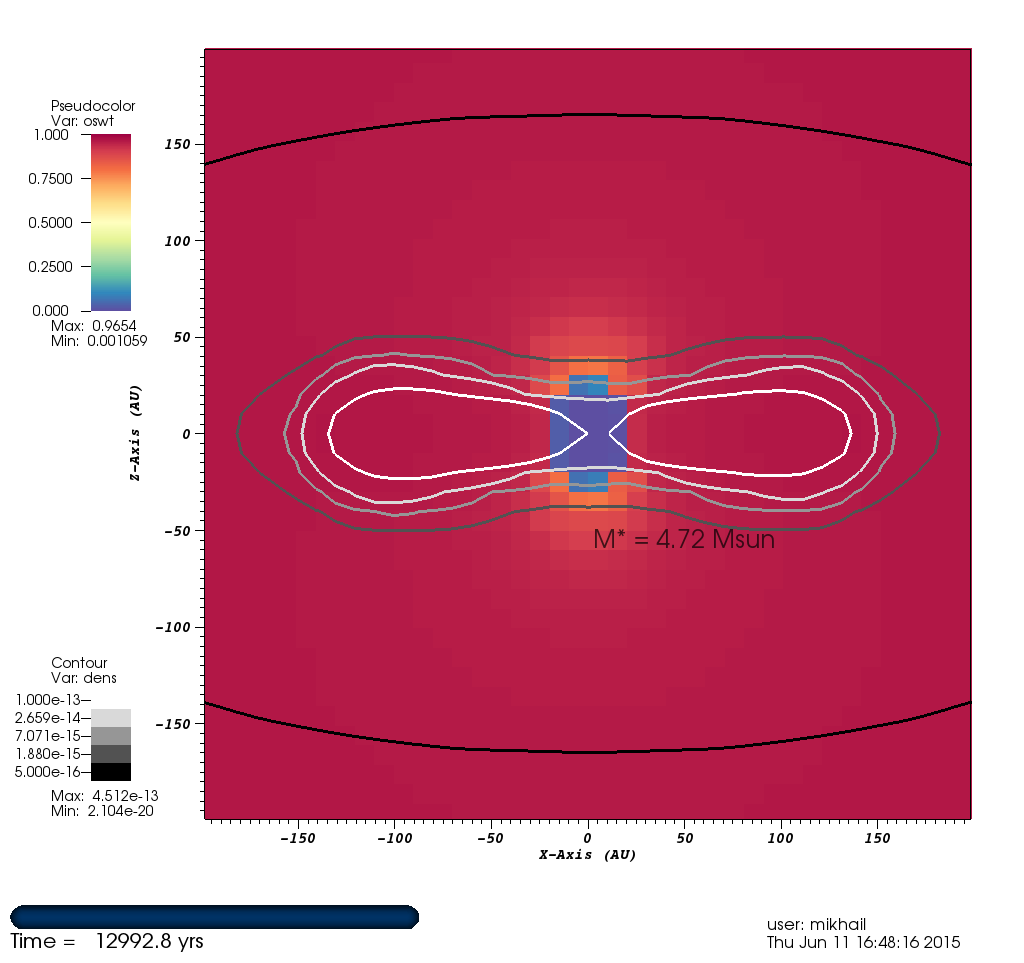
Figure 9: Irradiation¶

Figure 10: Matter-Radiation Coupling Timescale¶

Figure 11: Diffusion Timescale¶

Figure 12: Timescale Ratio¶

$$ t_{exch}/t_{diff} $$

Figure 13: Error Ratio¶

Figure 13: Toomre Q Parameter¶

The above shows the Toomre Q parameter at the same time as all the previous figures, at about 13000 years of evolution. The disk is still highly stable.

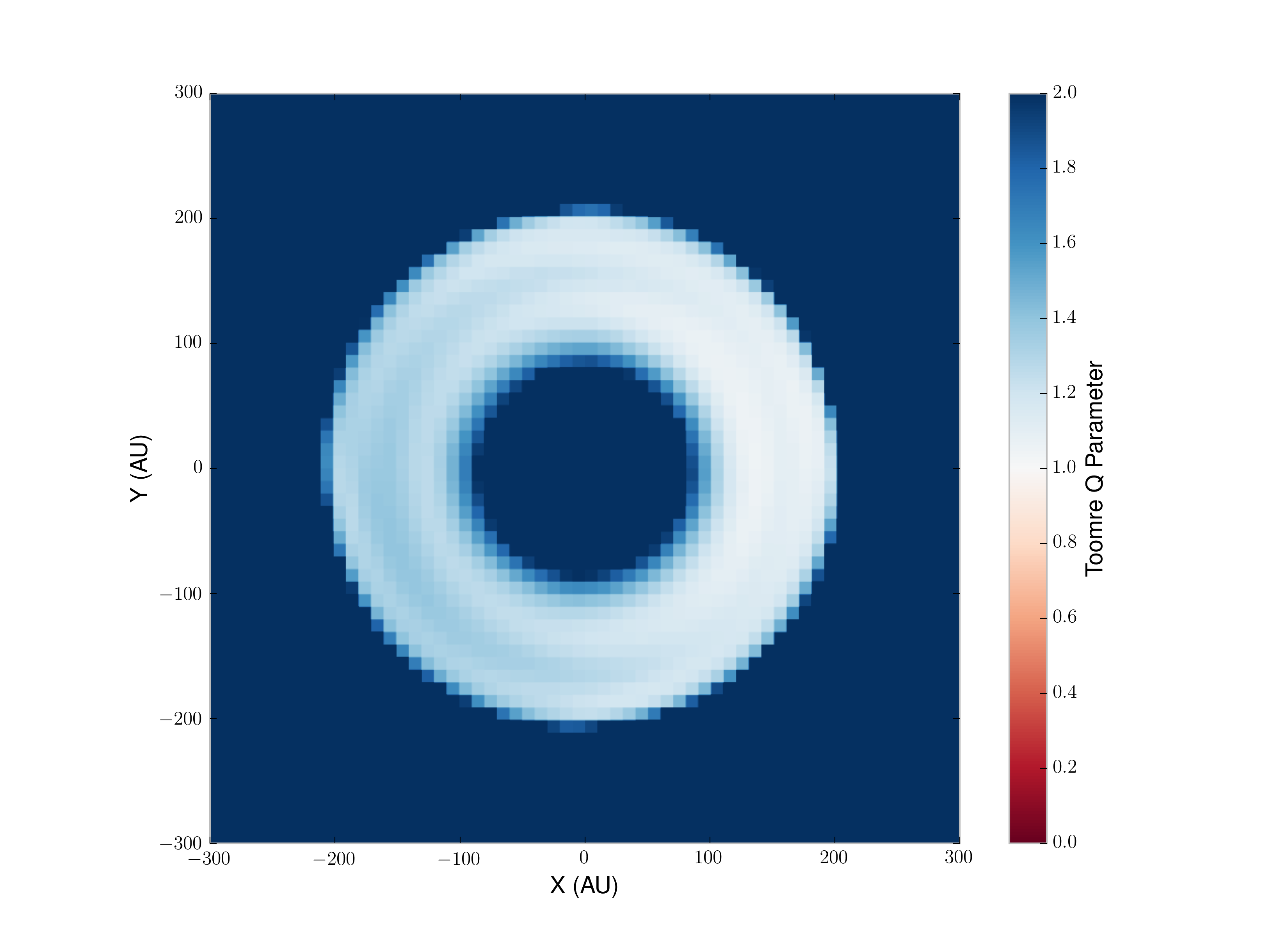The second image is of a "fast" simulation (dtmin = 5.0e7 seconds), evolved to 5.1e11 seconds, or 16161.3 years.