#!/usr/bin/env python
# coding: utf-8
# In[1]:
from IPython.display import Image
Image('../../Python_probability_statistics_machine_learning_2E.png',width=200)
# We saw with maximum likelihood estimation how we could use the
# principle of
# maximum likelihood to derive a formula of the data that
# would estimate the
# underlying parameters (say, $\theta$). Under that
# method, the parameter was
# fixed, but unknown. If we change our
# perspective slightly and consider the
# underlying parameter as a random
# variable in its own right, this leads to
# additional flexibility in
# estimation. This method is the simplest of the family
# of Bayesian
# statistical methods and is most closely related to maximum
# likelihood
# estimation. It is very popular in communications and signal
# processing
# and is the backbone of many important algorithms in those areas.
# Given that the parameter $\theta$ is also a random variable, it has a
# joint
# distribution with the other random variables, say,
# $f(x,\theta)$. Bayes'
# theorem gives the following:
#
# $$
# \mathbb{P}(\theta|x) =
# \frac{\mathbb{P}(x|\theta)\mathbb{P}(\theta)}{\mathbb{P}(x)}
# $$
#
# The $\mathbb{P}(x|\theta)$ term is the usual likelihood term we have
# seen
# before. The term in the denominator is *prior* probability of the data $x$
# and
# it explicitly makes a very powerful claim: even before collecting or
# processing
# any data, we know what the probability of that data is. The
# $\mathbb{P}(\theta)$ is the prior probability of the
# parameter. In other words,
# regardless of the data that is collected, this is
# the probability of the
# parameter itself.
#
# In a particular application, whether or not you feel
# justified making these
# claims is something that you have to reconcile for
# yourself and the problem at
# hand. There are many persuasive philosophical
# arguments one way or the other,
# but the main thing to keep in mind when applying
# any method is whether or not
# the assumptions are reasonable for the problem at
# hand.
#
# However, for now, let's just assume that we somehow have
# $\mathbb{P}(\theta)$
# and the next step is the maximizing of this expression over
# the $\theta$.
# Whatever results from that maximization is the maximum
# a-posteriori (MAP)
# estimator for $\theta$. Because the maximization takes place
# with respect to
# $\theta$ and not $x$, we can ignore the $\mathbb{P}(x)$ part. To
# make things
# concrete, let us return to our original coin flipping problem. From
# our
# earlier analysis, we know that the likelihood function for this problem is
# the following:
#
# $$
# \ell(\theta) := \theta^k (1-\theta)^{ (n-k) }
# $$
#
# where the probability of the coin coming up heads is $\theta$. The
# next step is
# the prior probability, $\mathbb{P}(\theta)$. For this example, we
# will choose
# the $\beta(6,6)$ distribution (shown in the top left panel of
# [Figure](#fig:MAP_001)). The $\beta$ family of distributions is a gold mine
# because it allows for a wide variety of distributions using few input
# parameters. Now that we have all the ingredients, we turn to maximizing the
# posterior function, $\mathbb{P}(\theta|x)$. Because the logarithm is convex, we
# can use it to make the maximization process easier by converting the product to
# a sum without changing the extrema that we are looking for. Thus, we prefer the
# to work with the logarithm of $\mathbb{P}(\theta|x)$ as in the following.
#
# $$
# \mathcal{L} := \log \mathbb{P}(\theta|x) = \log \ell(\theta) +
# \log\mathbb{P}(\theta) - \log\mathbb{P}(x)
# $$
#
# This is tedious to do by hand and therefore an excellent job
# for Sympy.
# In[7]:
import numpy as np
import sympy
from sympy import stats as st
from sympy.abc import p,k,n
# setup objective function using sympy.log
obj=sympy.expand_log(sympy.log(p**k*(1-p)**(n-k)*
st.density(st.Beta('p',6,6))(p)))
# use calculus to maximize objective
sol=sympy.solve(sympy.simplify(sympy.diff(obj,p)),p)[0]
sol
# which means that our MAP estimator of $\theta$ is the following:
#
# $$
# \hat{\theta}_{MAP} = \frac{k+5}{n+10}
# $$
#
# where $k$ is the number of heads in the sample. This is obviously a
# biased
# estimator of $\theta$,
#
# $$
# \mathbb{E}(\hat{\theta}_{MAP}) = \frac{5+n \theta}{10 +n} \neq \theta
# $$
#
# But is this bias *bad*? Why would anyone want a biased estimator?
# Remember that
# we constructed this entire estimator using the idea of the prior
# probability of
# $\mathbb{P}(\theta)$ which *favors* (biases!) the estimate
# according to the
# prior. For example, if $\theta=1/2$, the MAP estimator
# evaluates to
# $\hat{\theta}_{MAP}=1/2$. No bias there! This is because the peak
# of the prior
# probability is at $\theta=1/2$.
#
# To compute the corresponding variance for this
# estimator, we need this
# intermediate result,
#
# $$
# \mathbb{E}(\hat{\theta}_{MAP}^2) =\frac{25 +10 n \theta + n \theta((n-1)
# p+1)}{(10+n)^2}
# $$
#
# which gives the following variance,
#
# $$
# \mathbb{V}(\hat{\theta}_{MAP}) = \frac{n (1-\theta) \theta}{(n+10)^2}
# $$
#
# Let's pause and compare this to our previous maximum likelihood (ML) estimator
# shown below:
#
# $$
# \hat{\theta}_{ML} = \frac{1}{n} \sum_{i=1}^n X_i = \frac{k}{n}
# $$
#
# As we discussed before, the ML-estimator is unbiased with the
# following
# variance.
#
# $$
# \mathbb{V}(\hat{\theta}_{ML}) = \frac{\theta(1-\theta)}{n}
# $$
#
# How does this variance compare to that of the MAP? The ratio of the
# two is the
# following:
#
# $$
# \frac{\mathbb{V}(\hat{\theta}_{MAP})}{\mathbb{V}(\hat{\theta}_{ML})}=\frac{n^2}{(n+10)^2}
# $$
#
# This ratio shows that the variance for the MAP-estimator is smaller
# than that
# of the the ML-estimator. This is payoff for having a biased
# MAP-estimator --- it
# requires fewer samples to estimate if the underlying
# parameter is consistent
# with the prior probability. If not, then it will take
# more samples to pull the
# estimator away from the bias. In the limit as $n
# \rightarrow \infty$, the ratio
# goes to one. This means that the benefit of the
# reduced variance vanishes with
# enough samples.
#
# The above discussion admits a level of arbitrariness via the
# prior
# distribution. We don't have to choose just one prior, however. The
# following shows how we can use the previous posterior distribution as the
# prior
# for the next posterior distribution,
#
# $$
# \mathbb{P}(\theta|x_{k+1}) =
# \frac{\mathbb{P}(x_{k+1}|\theta)\mathbb{P}(\theta|x_k)}{\mathbb{P}(x_{k+1})}
# $$
#
# This is a very different strategy because we are using every data
# sample $x_k$
# as a parameter for the posterior distribution instead of lumping
# all the samples
# together in a summation (this is where we got the $k$
# term in the prior case).
# This case is much harder to analyze because now
# every incremental posterior
# distribution is itself a random function because of
# the injection of the $x$
# random variable. On the other hand, this is more in
# line with more general
# Bayesian methods because it is clear that the output of
# this estimation process
# is a posterior distribution function, not just a single
# parameter estimate.
# [Figure](#fig:MAP_001) illustrates this method. The graph
# in the top row, far
# left shows the prior probability ($\beta(6,6)$) and the dot
# on the top shows the
# most recent MAP-estimate for $\theta$. Thus, before we
# obtain any data, the peak
# of the prior probability is the estimate. The next
# graph to right shows the
# effect of $x_0=0$ on the incremental prior
# probability. Note that the estimate
# has barely moved to the left. This is
# because the influence of the data has not
# caused the prior probability to drift
# away from the original
# $\beta(6,6)$-distribution. The first two rows of the
# figure all have $x_k=0$
# just to illustrate how far left the original prior
# probability can be moved by
# those data. The dots on the tops of the sub-graphs
# show how the MAP estimate
# changes frame-by-frame as more data is incorporated.
# The remaining graphs,
# proceeding top-down, left-to-right show the incremental
# change in the prior
# probability for $x_k=1$. Again, this shows how far to the right
# the estimate
# can be pulled from where it started. For this example, there
# are an equal number
# of $x_k=0$ and $x_k=1$ data, which corresponds
# to $\theta=1/2$.
#
#
#
#
#
# The prior probability is the $\beta(6,6)$
# distribution shown in the top left panel. The dots near the peaks of each of the
# subgraphs indicate the MAP estimate at that frame
#  #
#
#
#
# **Programming Tip.**
# The following is a quick paraphrase of how [Figure](#fig:MAP_001) was
# constructed. The first step is to recursively create the
# posteriors from the
# data. Note the example data is sorted
# to make the progression easy to see as a
# sequence.
# In[3]:
from sympy.abc import p,x
from sympy.stats import density, Beta, Bernoulli
prior = density(Beta('p',6,6))(p)
likelihood=density(Bernoulli('x',p))(x)
data = (0,0,0,0,0,0,0,1,1,1,1,1,1,1,1)
posteriors = [prior]
for i in data:
posteriors.append(posteriors[-1]*likelihood.subs(x,i))
# With the posteriors in hand, the next step
# is to compute the peak values at
# each frame using the
# `fminbound` function from Scipy's `optimize` module.
# In[4]:
from matplotlib.pylab import subplots
from scipy.optimize import fminbound
fig,ax = subplots(4,4,sharex=True,
subplot_kw={
'yticks':[],
'xticks':[0,0.5,1],
'xticklabels':[0,0.5,1]
}
)
fig.set_size_inches((8,8))
pvals = np.linspace(0,1,100)
mxvals = []
for i,j in zip(ax.flat,posteriors):
i.plot(pvals,sympy.lambdify(p,j)(pvals),color='k')
mxval = fminbound(sympy.lambdify(p,-j),0,1)
mxvals.append(mxval)
h = i.axis()[-1]
i.axis(ymax=h*1.3)
i.plot(mxvals[-1],h*1.2,'ok')
i.plot(mxvals[:-1],[h*1.2]*len(mxvals[:-1]),'o')
# The [Figure](#fig:MAP_002) is the same as [Figure](#fig:MAP_001) except that
# the
# initial prior probability is the $\beta(1.3,1.3)$-distribution, which has a
# wider lobe that the $\beta(6,6)$-distribution. As shown in the figure, this
# prior has the ability to be swayed more violently one way or the other based on
# the $x_k$ data that is incorporated. This means that it can more quickly adapt
# to data that is not so consistent with the initial prior and thus does not
# require a large amount of data in order to *unlearn* the prior probability.
# Depending on the application, the ability to unlearn the prior probability or
# stick with it is a design problem for the analyst. In this example, because the
# data are representative of a $\theta=1/2$ parameter, both priors eventually
# settle on an estimated posterior that is about the same. However, if this had
# not been the case ($\theta \neq 1/2$), then the second prior
# would have
# produced a better estimate for the same amount of data.
#
#
#
#
#
#
#
#
#
#
# **Programming Tip.**
# The following is a quick paraphrase of how [Figure](#fig:MAP_001) was
# constructed. The first step is to recursively create the
# posteriors from the
# data. Note the example data is sorted
# to make the progression easy to see as a
# sequence.
# In[3]:
from sympy.abc import p,x
from sympy.stats import density, Beta, Bernoulli
prior = density(Beta('p',6,6))(p)
likelihood=density(Bernoulli('x',p))(x)
data = (0,0,0,0,0,0,0,1,1,1,1,1,1,1,1)
posteriors = [prior]
for i in data:
posteriors.append(posteriors[-1]*likelihood.subs(x,i))
# With the posteriors in hand, the next step
# is to compute the peak values at
# each frame using the
# `fminbound` function from Scipy's `optimize` module.
# In[4]:
from matplotlib.pylab import subplots
from scipy.optimize import fminbound
fig,ax = subplots(4,4,sharex=True,
subplot_kw={
'yticks':[],
'xticks':[0,0.5,1],
'xticklabels':[0,0.5,1]
}
)
fig.set_size_inches((8,8))
pvals = np.linspace(0,1,100)
mxvals = []
for i,j in zip(ax.flat,posteriors):
i.plot(pvals,sympy.lambdify(p,j)(pvals),color='k')
mxval = fminbound(sympy.lambdify(p,-j),0,1)
mxvals.append(mxval)
h = i.axis()[-1]
i.axis(ymax=h*1.3)
i.plot(mxvals[-1],h*1.2,'ok')
i.plot(mxvals[:-1],[h*1.2]*len(mxvals[:-1]),'o')
# The [Figure](#fig:MAP_002) is the same as [Figure](#fig:MAP_001) except that
# the
# initial prior probability is the $\beta(1.3,1.3)$-distribution, which has a
# wider lobe that the $\beta(6,6)$-distribution. As shown in the figure, this
# prior has the ability to be swayed more violently one way or the other based on
# the $x_k$ data that is incorporated. This means that it can more quickly adapt
# to data that is not so consistent with the initial prior and thus does not
# require a large amount of data in order to *unlearn* the prior probability.
# Depending on the application, the ability to unlearn the prior probability or
# stick with it is a design problem for the analyst. In this example, because the
# data are representative of a $\theta=1/2$ parameter, both priors eventually
# settle on an estimated posterior that is about the same. However, if this had
# not been the case ($\theta \neq 1/2$), then the second prior
# would have
# produced a better estimate for the same amount of data.
#
#
#
#
#
# For this example, the
# prior probability is the $\beta(1.3,1.3)$ distribution, which has a wider main
# lobe than the $\beta(6,6)$ distribution. The dots near the peaks of each of the
# subgraphs indicate the MAP estimate at that frame.
#  #
#
#
#
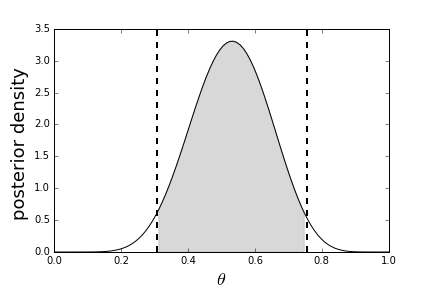
# Because we have the
# entire posterior density available, we can compute
# something that is closely
# related to the confidence interval we discussed
# earlier, except in this
# situation, given the Bayesian interpretation, it is
# called a *credible interval*
# or *credible set*. The idea is that we want to
# find a symmetric interval around
# the peak that accounts for 95% (say) of the
# posterior density. This means that
# we can then say the probability that the
# estimated parameter is within the
# credible interval is 95%. The computation
# requires significant numerical
# processing because even though we have the
# posterior density in hand, it is hard
# to integrate analytically and requires
# numerical quadrature (see Scipy's
# `integrate` module). [Figure](#fig:MAP_003)
# shows extent of the interval and
# the shaded region under the posterior density
# that accounts for 95%.
#
#
#
#
#
#
#
#
#
#
# Because we have the
# entire posterior density available, we can compute
# something that is closely
# related to the confidence interval we discussed
# earlier, except in this
# situation, given the Bayesian interpretation, it is
# called a *credible interval*
# or *credible set*. The idea is that we want to
# find a symmetric interval around
# the peak that accounts for 95% (say) of the
# posterior density. This means that
# we can then say the probability that the
# estimated parameter is within the
# credible interval is 95%. The computation
# requires significant numerical
# processing because even though we have the
# posterior density in hand, it is hard
# to integrate analytically and requires
# numerical quadrature (see Scipy's
# `integrate` module). [Figure](#fig:MAP_003)
# shows extent of the interval and
# the shaded region under the posterior density
# that accounts for 95%.
#
#
#
#
#
# The credible interval
# in Bayesian maximum a-posteriori is the interval corresponding to the shaded
# region in the posterior density.
#  #
#
#
#
 #
#
#
#
# **Programming Tip.**
# The following is a quick paraphrase of how [Figure](#fig:MAP_001) was
# constructed. The first step is to recursively create the
# posteriors from the
# data. Note the example data is sorted
# to make the progression easy to see as a
# sequence.
# In[3]:
from sympy.abc import p,x
from sympy.stats import density, Beta, Bernoulli
prior = density(Beta('p',6,6))(p)
likelihood=density(Bernoulli('x',p))(x)
data = (0,0,0,0,0,0,0,1,1,1,1,1,1,1,1)
posteriors = [prior]
for i in data:
posteriors.append(posteriors[-1]*likelihood.subs(x,i))
# With the posteriors in hand, the next step
# is to compute the peak values at
# each frame using the
# `fminbound` function from Scipy's `optimize` module.
# In[4]:
from matplotlib.pylab import subplots
from scipy.optimize import fminbound
fig,ax = subplots(4,4,sharex=True,
subplot_kw={
'yticks':[],
'xticks':[0,0.5,1],
'xticklabels':[0,0.5,1]
}
)
fig.set_size_inches((8,8))
pvals = np.linspace(0,1,100)
mxvals = []
for i,j in zip(ax.flat,posteriors):
i.plot(pvals,sympy.lambdify(p,j)(pvals),color='k')
mxval = fminbound(sympy.lambdify(p,-j),0,1)
mxvals.append(mxval)
h = i.axis()[-1]
i.axis(ymax=h*1.3)
i.plot(mxvals[-1],h*1.2,'ok')
i.plot(mxvals[:-1],[h*1.2]*len(mxvals[:-1]),'o')
# The [Figure](#fig:MAP_002) is the same as [Figure](#fig:MAP_001) except that
# the
# initial prior probability is the $\beta(1.3,1.3)$-distribution, which has a
# wider lobe that the $\beta(6,6)$-distribution. As shown in the figure, this
# prior has the ability to be swayed more violently one way or the other based on
# the $x_k$ data that is incorporated. This means that it can more quickly adapt
# to data that is not so consistent with the initial prior and thus does not
# require a large amount of data in order to *unlearn* the prior probability.
# Depending on the application, the ability to unlearn the prior probability or
# stick with it is a design problem for the analyst. In this example, because the
# data are representative of a $\theta=1/2$ parameter, both priors eventually
# settle on an estimated posterior that is about the same. However, if this had
# not been the case ($\theta \neq 1/2$), then the second prior
# would have
# produced a better estimate for the same amount of data.
#
#
#
#
#
#
#
#
#
#
# **Programming Tip.**
# The following is a quick paraphrase of how [Figure](#fig:MAP_001) was
# constructed. The first step is to recursively create the
# posteriors from the
# data. Note the example data is sorted
# to make the progression easy to see as a
# sequence.
# In[3]:
from sympy.abc import p,x
from sympy.stats import density, Beta, Bernoulli
prior = density(Beta('p',6,6))(p)
likelihood=density(Bernoulli('x',p))(x)
data = (0,0,0,0,0,0,0,1,1,1,1,1,1,1,1)
posteriors = [prior]
for i in data:
posteriors.append(posteriors[-1]*likelihood.subs(x,i))
# With the posteriors in hand, the next step
# is to compute the peak values at
# each frame using the
# `fminbound` function from Scipy's `optimize` module.
# In[4]:
from matplotlib.pylab import subplots
from scipy.optimize import fminbound
fig,ax = subplots(4,4,sharex=True,
subplot_kw={
'yticks':[],
'xticks':[0,0.5,1],
'xticklabels':[0,0.5,1]
}
)
fig.set_size_inches((8,8))
pvals = np.linspace(0,1,100)
mxvals = []
for i,j in zip(ax.flat,posteriors):
i.plot(pvals,sympy.lambdify(p,j)(pvals),color='k')
mxval = fminbound(sympy.lambdify(p,-j),0,1)
mxvals.append(mxval)
h = i.axis()[-1]
i.axis(ymax=h*1.3)
i.plot(mxvals[-1],h*1.2,'ok')
i.plot(mxvals[:-1],[h*1.2]*len(mxvals[:-1]),'o')
# The [Figure](#fig:MAP_002) is the same as [Figure](#fig:MAP_001) except that
# the
# initial prior probability is the $\beta(1.3,1.3)$-distribution, which has a
# wider lobe that the $\beta(6,6)$-distribution. As shown in the figure, this
# prior has the ability to be swayed more violently one way or the other based on
# the $x_k$ data that is incorporated. This means that it can more quickly adapt
# to data that is not so consistent with the initial prior and thus does not
# require a large amount of data in order to *unlearn* the prior probability.
# Depending on the application, the ability to unlearn the prior probability or
# stick with it is a design problem for the analyst. In this example, because the
# data are representative of a $\theta=1/2$ parameter, both priors eventually
# settle on an estimated posterior that is about the same. However, if this had
# not been the case ($\theta \neq 1/2$), then the second prior
# would have
# produced a better estimate for the same amount of data.
#
#
#
#
#
#  #
#
#
#
# Because we have the
# entire posterior density available, we can compute
# something that is closely
# related to the confidence interval we discussed
# earlier, except in this
# situation, given the Bayesian interpretation, it is
# called a *credible interval*
# or *credible set*. The idea is that we want to
# find a symmetric interval around
# the peak that accounts for 95% (say) of the
# posterior density. This means that
# we can then say the probability that the
# estimated parameter is within the
# credible interval is 95%. The computation
# requires significant numerical
# processing because even though we have the
# posterior density in hand, it is hard
# to integrate analytically and requires
# numerical quadrature (see Scipy's
# `integrate` module). [Figure](#fig:MAP_003)
# shows extent of the interval and
# the shaded region under the posterior density
# that accounts for 95%.
#
#
#
#
#
#
#
#
#
#
# Because we have the
# entire posterior density available, we can compute
# something that is closely
# related to the confidence interval we discussed
# earlier, except in this
# situation, given the Bayesian interpretation, it is
# called a *credible interval*
# or *credible set*. The idea is that we want to
# find a symmetric interval around
# the peak that accounts for 95% (say) of the
# posterior density. This means that
# we can then say the probability that the
# estimated parameter is within the
# credible interval is 95%. The computation
# requires significant numerical
# processing because even though we have the
# posterior density in hand, it is hard
# to integrate analytically and requires
# numerical quadrature (see Scipy's
# `integrate` module). [Figure](#fig:MAP_003)
# shows extent of the interval and
# the shaded region under the posterior density
# that accounts for 95%.
#
#
#
#
#
#  #
#
#
#